ТЕОРЕМА ГИПОТЕЗ (ФОРМУЛА БЕЙЕСА).
Имеется полная группа несовместных гипотез Н1, Н2…Нn . Известны вероятности каждой из гипотез Р(Н1), Р(Н2), …, Р(Нn). Производится опыт и в его результате осуществляется некоторое событие А, вероятности которого по каждой из гипотез известны, т.е. известны Р(А/Н1), Р(А/Н2), …, Р(А/Нn).
Спрашивается какие вероятности имеют гипотезы Нi (i=1, 2, …, n) в связи с появлением события А? Другими словами, нас интересует условные вероятности Р(Нi/А) для каждой гипотезы.
Теорема гипотез. Вероятность гипотезы после испытания равна произведению вероятности гипотезы до испытания на соответствующую ей условную вероятность события, которое произошло при испытании деленному на полную вероятность этого события.
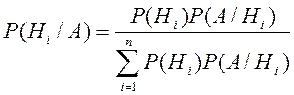 формула Бейеса.
формула Бейеса.
Доказательство. На основании аксиомы умножения вероятности имеем Р(А)Р(Нi /А)=Р(Нi) Р(А/Нi).
Разрешая это уравнение относительно Р(Нi/А), при условии, что Р(А)¹0, получим 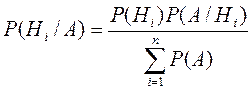 .
.
Выражая Р(А) с помощью формулы полной вероятности поучим доказываемое равенство
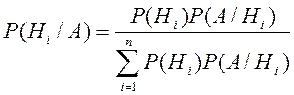 .
.
В частном случае, если все гипотезы Нi (i=1, 2, …, n) до испытания имеют одинаковую вероятность Р(Нi)= р, формула Бейеса принимает вид
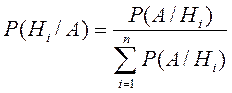 .
.
Дата добавления: 2016-03-05; просмотров: 1021;
