ФОРМУЛА ПОЛНОЙ ВЕРОЯТНОСТИ.
Пусть некоторое интересующее нас событие А может наступить или не наступить с одним из ряда несовместных событий Н1, Н2…Нn, составляющих полную группу. События такого рода обычно называют гипотезами. Вероятности всех гипотез известны, т.е. даны Р(Н1), Р(Н2), …, Р(Нn). Известны также условные вероятности наступления события А при осуществлении каждой из указательных гипотез, т.е. даны Р(А/Н1), Р(А/Н2), …, Р(А/Нn). Вероятность интересующих нас события А определяется по следующей теореме.
Теорема. Вероятность события А, которое может произойти вместе с одной из гипотез Н1, Н2…Нn равна сумме парных произведений вероятностей каждой из этих гипотез на отвечающее им условные вероятности наступления события А.
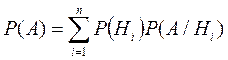 формула полной вероятности
формула полной вероятности
Доказательство. Так как гипотезы Н1, Н2…Нn образуют полную группу, то событие А можно представить в виде следующей сумме событий
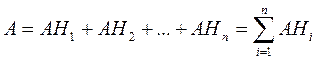
Поскольку события Нi несовместимы, т.е. события АНi (i=1,2, …,n) тоже несовместны. Это обстоятельство позволяет применить для определения вероятности событие А теорему сложения вероятностей несовместных событий:
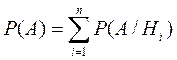
Вероятность же произведения событий А и Нi , находится по аксиоме умножения вероятностей:
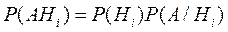
Подставляя последнее выражение получим:
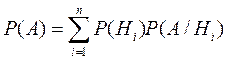
Дата добавления: 2016-03-05; просмотров: 961;
