ТЕОРЕМА СЛОЖЕНИЯ ВЕРОЯТНОСТЕЙ

Теорема. Вероятность появления одного или нескольких несовместных событий равна сумме вероятностей этих событий : Р(А₁+А₂+…+А_n)

Доказательство: Пусть теорема имеет место для n-1 событий

Р(А₁+ …+А_n-1)=Р(А₁)+Р…+Р(А_n-1), обозначим А₁+…+А_n-1=с, тогда в силу аксиомы 4 Р(А₁+ …+А_n-1 +А_n)=Р(С+А_n)=Р(С)+Р(А_n), по

Р(С)= Р(А₁+ …+А_n-1)=

Следовательно Р(А₁+ …+А_n-1 +А_n)= Р(А₁)+…+Р(А_n-1)+ Р(А_n)

Если число несовместных событий, входящих в сумму будет бесконечно большим, то распространение правила сложения вероятностей на этот случай устанавливается аксиоматически.

Аксиома 5. Вероятность суммы бесконечно большого числа несовместных событий равна сумме вероятностей этих событий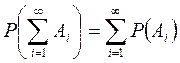

Следствие 1. Если события А₁, А₂, …, А_n образуют полную группу несовместных событий, то сумма их вероятностей равна единице Р(А₁)+Р(А₂)+…+Р(А_n)=1

Доказательство: Так как события А₁, А₂, …, А_n образуют полную группу событий, то их сумма А₁+А₂+…+А_n - является достоверным событием, поэтому Р(А₁+А₂+…+А_n)=1 Þ Р(А₁)+Р(А₂)+…+ Р(А_n)=1

Следствие 2. Сумма вероятностей противоположных событий равна единице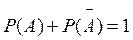

Доказательства не требуется, т.к 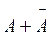- частный случай полной группы несовместных событий. Поэтому следствие 2 вытекает из следствия 1