Случайные события. Классификация событий. Сумма и произведение событий.

КРАТКАЯ ИСТОРИЧЕСКАЯ СПРАВКА

Первые работы, в которых зарождались основные понятия теории вероятностей, представляли собой попытки создания теории азартных игр (Кардано, Гюйгенс, Паскаль, Ферма и другие в XVI – XVII вв).

Следующий этап развития теории вероятностей связан с именем Якоба Бернулли (1654-1705). Доказанная им теорема, получившая в последствии название «Закона больших чисел» была первым теоретическим обоснованием накопленных ранее фактов. Дальнейшими успехами теория вероятностей обязана Муавру, Лапласу, Гауссу, Пуассону и др.

Новый, наиболее плодотворный период связан с именами П.Л.Чебышева (1856-1922) и А.М.Ляпунова (1857-1918). В этот период теория вероятностей становится стройной математической наукой. Ее последующее развитие обязано в первую очередь русским и советским математикам (С.Н.Бернштейн, В.И.Романовским, А.Н.Колмогоров, А.Я.Хинчин, Б.В.Греденко и д.р.).

В настоящее время ведущая роль в создании новых ветвей теории вероятностей также принадлежит российским математикам.

ТЕМА 1. ВЕРОЯТНОСТЬ СЛУЧАЙНОГО СОБЫТИЯ.

Математическая наука, изучающая общие закономерности случайных явлении независимо от их конкретной природы и дающая методы количественной оценки влияния случайных факторов на различные явления, называется теорией вероятностей.

Случайные события. Классификация событий. Сумма и произведение событий.

В основе теории вероятностей, как и в основе любой другой науки, лежат некоторые определения, начальные понятия. При помощи этих понятий дается логическое определение последующих более сложных понятий.

В качестве одного из основных понятий, который оперирует теория вероятностей, является событие.

Событием в теории вероятностей называется всякий факт, который может произойти в результате опыта (испытания) A,B

Событиями принято обозначать большими буквами латинского алфавита.

Различные события отличаются между собой по степени возможности их появления и по характеру взаимосвязи.

Классификация событий:

- достоверным – называется событие, если оно наступает при всех опытах;

- невозможным – называется событие, которое не наступает при всех опытах;

- возможным или случайным- называется событие, которое в результате опыта может как появиться так и не появиться;

- равновозможными – называются два или несколько событий, если условия их появления одинаковы и нет основания утверждать, что какое-либо из них в результате опыта имеет больше шансов появиться чем другое;

- совместными – называются два события Аи В,если появление одного из них не исключает появление другого;

- несовместными - называются два события Аи В,если появление одного из них исключает появление другого

- группой совместных событий – называется группа событий -,,,..

если хотя бы два события входящие в группу совместны.

- группой несовместных событий – называется группа событий - ,,,.. если события входящие в группу попарно несовместны.

- полная группа – несколько событий, если в результате опыта обязательно наступает хотя бы одно из них. На практике широко применение находит полная группа несовместных событий.

- противоположные – два несовместных события, образующие полную группу A и .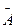

При разработке аппарата и методике исследования случайных событий в ТВ очень важным понятием является понятие суммы и произведения событий.

Суммой, или объединением, нескольких событий называется событие, состоящее наступлении хотя бы одного из этих событий:

Произведением, или совмещением, нескольких событий называется событие, состоящее в совместном появлении всех этих событий:

S=ABC…N

Из определений суммы и произведения следует:

А+А=А А*А=А.

В некоторых случаях можно наблюдать, что наступление одного события В влечет за собой наступление другого события А, т.е. событие В содержится в событииА.В этом случае

А+В=А А*В=В ВÌА

ГЕОМЕТРИЧЕСКАЯ ИНТЕРПРИТАЦИЯ СУММЫ И УМНОЖЕНИЯ.