ТЕОРЕМА СЛОЖЕНИЯ ВЕРОЯТНОСТИ ДЛЯ СОВМЕСТНЫХ СОБЫТИЙ.
Пользуясь теоремой сложения вероятности для несовместных событий, вместе с теоремой умножения докажем следующую теорему сложения вероятностей для совместных событий.
Теорема. Вероятность проявления хотя бы одного из двух совместных событий равна сумме вероятности этих событий без вероятности их совместного проявления
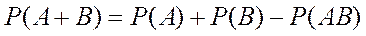
Доказательство. Для наступления А достаточно, чтобы произошло хотя бы одно из следующих несовместных событий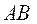 
и 
.
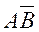Аналогично, для наступления В достаточно 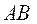и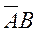 
.
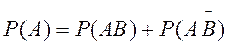
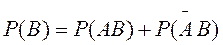
Для наступления хотя бы одного из событий А или В достаточно, чтобы произошло одно из трех попарно несовместных событий
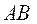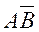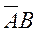, , . Поэтому
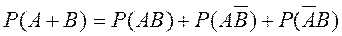
Сложив равенство для Р(А) и Р(В), найдем
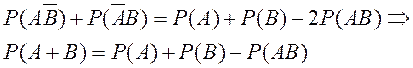
Геометрическая интерпретация.
Методом полной математической индукции
полученную формулу можно обобщить на
случай вероятности суммы произвольного
числа совместных событий.
При этом будет иметь:
Р(А1+А2+…+Аn)= Р(А1)+Р(А2)+…+ Р(Аn)-Р(А1А2)- Р(А1А3)- …-Р(Аn-1Аn)+ Р(А1А2А3)+…+Р(Аn-2Аn-1Аn)-…+(-1)n+1Р(А1А2...Аn).
Последнее соотношение слишком громоздко, поэтому лучше перейти к противоположному событию
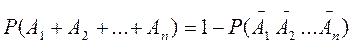
Дата добавления: 2016-03-05; просмотров: 904;