ТЕОРЕМА УМНОЖЕНИЯ ВЕРОЯТНОСТЕЙ.

Определение: Событие А называется независимым по отношению к событию В, если вероятность события А не зависит от того, произошло событие В или нет. В противном случае событие А называется зависимым от события В.

Условия независимости: =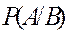

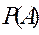
Условия зависимости: 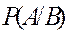¹

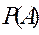
Теорема. Вероятность произведения, или совместного наступления, нескольких событий равна произведению вероятности одного из них на условные вероятности остальных событий, вычисленные в предложении, что все предшествующие события имели место:

Р(А₁А₂ …А_n)=Р(А₁)Р(А₂/А₁)…Р(А_n/А₁А₂…А_n-1)

Доказательство: Применим метод математической индукции.

Пусть теорема имеет место для n-1 событий

Р(А₁А₂ …А_n)=Р(А₁)Р(А₂/А₁)Р(А_n-1/А₁А₂…А_n-2),пусть С= А₁А₂ …А_n-1

Тогда в силу аксиомы 5 Р(А₁А₂ …А_n)= Р(С А_n)=Р(С)Р(А_n/С),по

Р(С)= Р(А₁А₂ …А_n-1)Þ Р(А₁А₂ …А_n)= Р(А₁)Р(А₂/А₁)…Р(А_n/А₁А₂…А_n-1)

Следствие 1. Если событие А не зависит от события В, то и событие В не зависит от события А.

Доказательство: Так как А не зависит от В, то =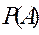

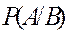
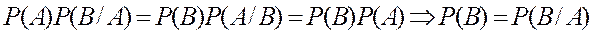
Определение: Два события называются независимыми, если появление одного из них не изменяет вероятности появление другого.

Определение позволяет распространить понятие независимости на случай произвольного числа событий.

Несколько событий называют независимыми в совокупности, если каждое из них и любая комбинация остальных событий, содержащая либо все остальные события, либо часть из них события независимые.

Следствие 2. Вероятность произведения независимых в совокупности событий равна произведению вероятности этих событий, т.е для независимых событий имеет место соотношение

Р(А₁А₂ А₃…А_n)=Р(А₁)Р(А₂)Р(А₃)…Р(А_n)