Вывод формулы Бернулли.

Производится n испытаний. Вероятность наступления события А в каждом Р(А)=р, а события 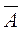с вероятностью .

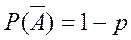Обозначим через А_i(i=1, 2, …, n)

Р(А₁)=Р(А₂)= … = Р(А_n) = р

.

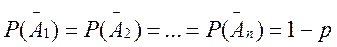
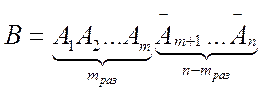Используя теорему сложения для независимых событий

.

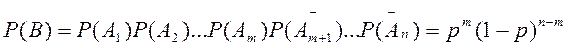Так как все комбинации событий, подобные комбинации В, являются несовместными событиями и нам безразлично, в какой именно последовательности появится событие А и в какой последовательности появится противоположное ему событие 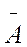, то применяя теорему сложения вероятностей для несовместных событий получим:

.

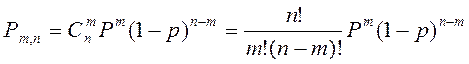Полученная формула носит название формулу Бернулли.

Так как события, состоящие в различном числе появления события А в серии из n испытаний, несовместны и образуют полную группу, то

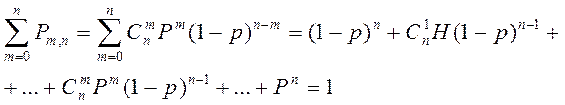
Обозначая 1-р=q, нетрудно заменить, что члены сумм совпадают с членами разложения бинома (q+p)ⁿ=qⁿ+C¹_npq^n-1+…+ C^m_np^mq^n-m +…+pⁿ=1.

В связи с этим распределение вероятностей называют биноминальным распределением.

Вывод производящей функции j_n(х)

j_n(х)=(q+рх)ⁿ = qⁿx⁰+C¹_npq^n-1x+…+ C^m_np^mq^n-mx^m+… + pⁿxⁿ.

Это функция обладает тем свойством, что коэффициент при х^m в разложении равен вероятности наступления события А ровно m раз в серии из n независимых испытаний, проводимых в переменных условиях. Так если вероятность появления событий А в i-м опыте Р(А_i) = p_i и вероятность не появления

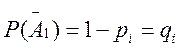, то вероятность того, что событие А появится ровно m раз в n независимых испытаниях равна коэффициенту np X^m в разложении по степеням Х производящей функции

j_n(х)=(q₁+р₁х) (q₂+р₂х)… (q_n+р_nх).

Определение.Наивероятнейшим числом m_i появления события А в n независимых испытаниях называется число, для которого вероятность Р_m,_n превышает или по крайней мере, не меньше вероятности каждого из остальных возможных испытаний.

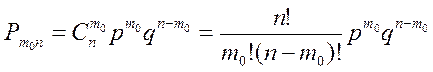
По определению Р_m0,n³ Р_m0-1,n; Р_m0,n³ Р_m0+1,n.

Подставив, в эти два неравенства их значения, полученные по формуле Бернулли и выполнив необходимые преобразования получим:

np-q£m₀£mp+p

Замечание. Длина интервала, определяемого неравенством равна 1. Поэтому если границы этого интервал есть дробные числа, то мы получаем одно замечание наивероятнейшего числа, если же границы являются целыми числами, то получаем два значения.

ТЕМА 3. ДИСКРЕТНЫЕ И НЕПРЕРЫВНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ. КЛАССИЧЕСКИЕ РАСПРЕДЕЛЕНИЯ.

1. Понятие случайной величины. Закон распределения вероятностей дискретной случайной величины.

Количественной характеристикой случайного результата опыта является случайная величина.

Случайной величиной называется величина, которая в результате опыта может принять то или иное (но только одно) значение, причем заранее до опыта неизвестно какое именно.

Случайные величины обозначают обычно заглавными буквами конца латинского алфавита – X, Y, Z, а их возможные значения соответствующими малыми – x, y, z.

Среди случайных величин, с которыми приходится встречаться в практике, можно выделить два основных типа: дискретные и непрерывные.

Дискретной случайной величиной называется такая величина, число возможных значений которое либо конечно, либо бесконечно счетное множество ( множество элементов, которые могут быть занумерованы)

Пример:

1) частота, полуосей при трех выстрелах у СВ возможны следующие значения x₁=0, x₂=1/3, x₃=2/3,x₄=3

2) число дефектных изучений в партии из n штук: у СВ возможны следующие значения n