Функция и плотность распределения.
Рассмотренный ряд распределения является удобной формой представления закона распределения, для дискретной СВ. однако ряд распределении вообще нельзя построить для непрерывной СВ.
Наиболее общей формой закона распределения СВ является функция распределения.
Функция распределения, или интегральным законом распределения, СВ Х называется задание вероятности выполнения неравенства Х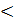 
х, рассматриваемой как функции аргумента х.
F(x)=P(Х 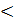х)
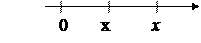Геометрическая интерпретация
Для дискретной СВ Х, которая может принимать значения х1; х2; …., хn функция распределения будет иметь вид F(X)=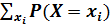 
.
График F(x) для дискретной СВ представляет собой ступенчатую ломаную линию. 
Свойства функции распределения.
Свойство 1.Функция распределения F(x) есть неотрицательная функция заключенная между нулем и единицей.
0≤ F(x)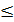 
1.
Свойство 2.Вероятность появления СВ в интервале [α,β), полузамкнутом слева равна разности значений функции распределения в концах интервала, т.е. P(α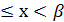 
)=F(β)-F(α).
Доказательство: рассмотрим три события
А состоящее в том, что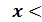 
β
Всостоящее в том, что 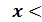α
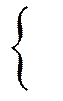С состоящее в том, что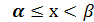 
Очевидно, что А=В+С, но Р(А)=Р(х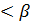 
)= F(β)
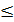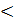F(β)= F(α)+Р(α х β)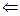 
Р(В)=Р(х 
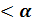)= F(α)
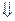
P(α 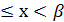)=F(β)-F(α). Р(С)=Р(α )
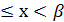Свойство 3.Функция распределения СВ есть неубывающая функция, т.е. при α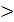 
β F(β) 
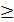F(α), вытекает из свойства 2.
Свойство 4.На минус ∞функция распределения равна 0, а на плюс ∞
Дата добавления: 2016-03-05; просмотров: 885;