Классические распределения.
Биномиальное распределение.
СВ Х выражает число проявлений события А при n независимых испытаниях, проводимых в одинаковых условиях. Вероятность проявления события А постоянно и равна Р; q=1-р. Возможными значениями СВ Х являются х0=0, х1=1, …, хn=n.
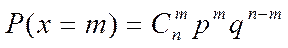
- (m=0,1,…,n) – формула Бернулли.
Распределения дискретной СВ для которой ряд распределения задается этой формулой называется биномиальным.
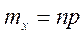 ;
; 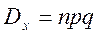 ,
, 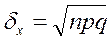
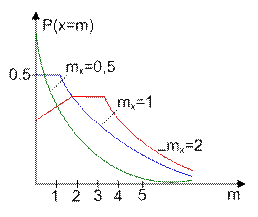
Распределения Пуассона.
Пример: число вызовов на ТЛФ - станции за некоторое время t. Распределение дискретной СВ Х описываемой формулой 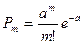 и называется распределение Пуассона. Распределение Пуассона зависит от одного параметра a, который является МОЖ СВ Х (mx=a).
и называется распределение Пуассона. Распределение Пуассона зависит от одного параметра a, который является МОЖ СВ Х (mx=a).
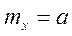 ;
; 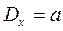 ;
;
Когда в биномиальном распределении 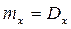 ; т.е.
; т.е. 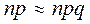 можно использовать, как приближенную формулу
можно использовать, как приближенную формулу 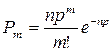 .
.
Равномерное распределение.
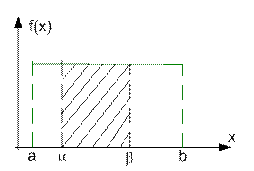
Непрерывное СВ Х имеет равномерное распределение на отрезке[a;b], если на этом отрезке плотность распределения СВ постоянна, а вне его равно нулю, т.е.
0 при x<a
f(x)= c при a£x£b
0 при x>b , где C = const


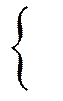
0 при x<a
F(x)= 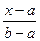 при a£x£b
при a£x£b
1 при x>b

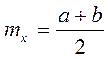 ;
;  ;
;  .
.
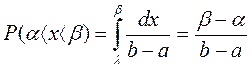
Показательное распределение.
В практических приложениях теории вероятностей, особенно в теории массового обслуживания, исследований операций, в физики, биологии и т.д. часто имеют дело со СВ, имеющими так называемое экспоненциальное или показательное распределение. Непрерывная СВ распределена по показательному закону, если ее плотность вероятности имеет вид:
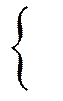
le-lx при x³0
f(x)= 0 при x<0



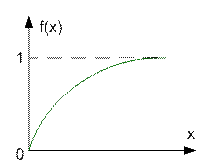
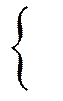
1-e-lx при x³0
F(x)= 0 при x<0
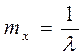 ,
, 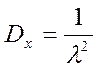 ,
,  .
.
Нормальное распределение.
Среди распределений непрерывных СВ центральное место занимает нормальный закон (закон Гаусса), плотность вероятности которого имеет вид:
f(x) 
 ,
,
где mx и 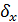 - параметр нормального распределения. Нормальный закон распределения очень широко распространен в задачах практики. Он проявляется в тех случаях, когда СВ Х является результатом действия большого числа различных факторов. Примеры: отклонение действительных размеров деталей, обработанных на станке, ошибки при измерении, отклонение при стрельбе и т.д.
- параметр нормального распределения. Нормальный закон распределения очень широко распространен в задачах практики. Он проявляется в тех случаях, когда СВ Х является результатом действия большого числа различных факторов. Примеры: отклонение действительных размеров деталей, обработанных на станке, ошибки при измерении, отклонение при стрельбе и т.д.
Основная особенность – он является предельным законом, к которому приближаются другие законы распределения:
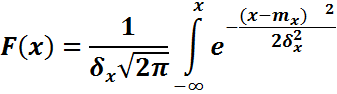
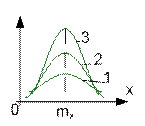
M[x]=mx- МОЖ 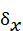 =2,5 ; 2.
=2,5 ; 2. 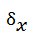 =1; 3.
=1; 3. 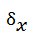 =0,4.
=0,4.
D[x]= 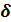 x2– дисперсия
x2– дисперсия 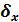 - СКО
- СКО
Вероятность попадания СВ имеющей нормальное распределение в промежутке [α;β] вычисляется с помощью функции Лапласа:
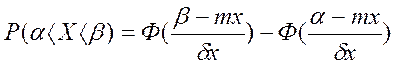
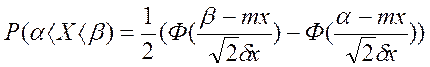
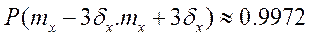
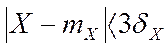 - практически достоверно (правило 3 сигм).
- практически достоверно (правило 3 сигм).
Дата добавления: 2016-03-05; просмотров: 1165;
