Законом распределения СВ называется всякое соотношение, устанавливающее связь между областями возможных значений системы СВ и вероятностями появления системы в этих областях.
| х1 | х2 | … | xn | |
| y1 | P11 | P21 | … | Pn1 |
| y2 | P12 | P22 | … | … |
| … | … | P | … | …. |
| yn | P1m | P2m | … | Pnm |
Такая таблица называется таблицей распределения
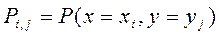
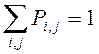
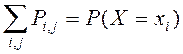
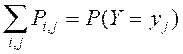
Функция распределения системы двух СВ называется функцией двух аргументов F(x,y), равная вероятности совместного выполнения двух неравенств, т.е. F(x,y)=P (X ‹ x, Y ‹ y).
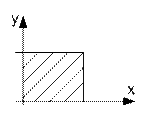
Геометрическая интерпретация: попадание в левый нижний бесконечный квадрат.
Свойство 1. Если один из аргументов стремится к плюс бесконечности, то функция распределения системы стремится к функции распределения одной СВ, соответствующей другому аргументу
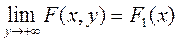
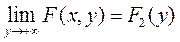
Свойство 2. Если оба аргумента стремятся к плюс бесконечности, то функция распределения системы стремится к единице, т.е.
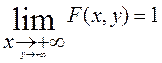
Свойство 3. При стремлении одного или обоих аргументов к минус бесконечности функция распределения стремится к нулю
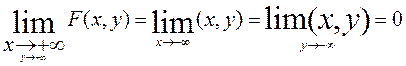
Свойство 4. Функция распределения является неубывающей функцией по каждому аргументу.
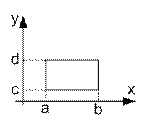
Свойство 5. Вероятность попадания случайной точки (X;Y) в произвольный прямоугольник со сторонами, параллельными координатными осями, вычисляется по формуле
P(a≤X≤b ; c≤Y≤d)=F(b,d)-F(a,d)-F(b,c)+F(a,c)
Функция 
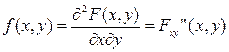 называется плотностью распределения системы непрерывных СВ(x,y).
называется плотностью распределения системы непрерывных СВ(x,y).
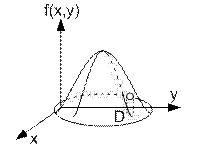
(Поверхность распределения)
Геометрически вероятность попадания в область D изображается объемом цилиндрического тела, ограниченного поверхностью распределения
и определяющеюся на эту область 
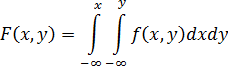
Свойство 1. Плотность распределения есть функция неотрицательная
f(X,Y)≥0.
Свойство 2. Двойной несобственный интеграл с бесконечными пределами от плотности распределения системы равен единице
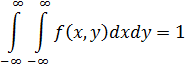
Дата добавления: 2016-03-05; просмотров: 912;
