Его точки описывают траектории, параллельные некоторой неподвижной плоскости.
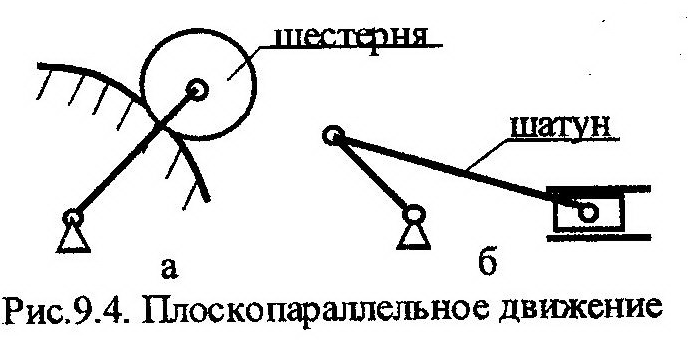
| Плоское движение совершают многие части механизмов и машин, например, шестерня и шатун, изображенные на рис. 9.4. При таком движении все сечения тела, параллельные неподвижной плоскости, будут двигаться одинаково. Поэтому, уравнениями плоского движения тела будут выражения, описывающие |
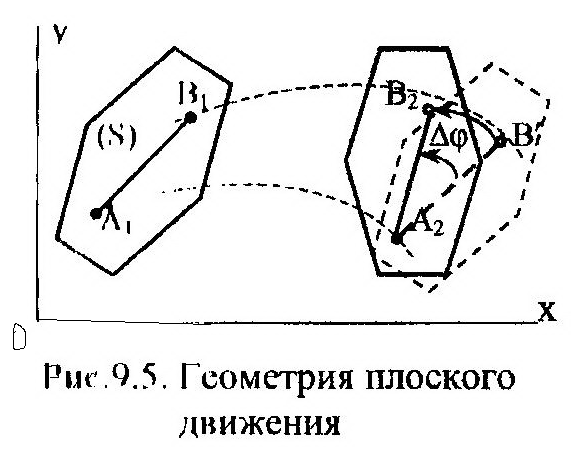
движение любой прямой АВ, взятой в этом сечении (рис. 9.5). Очевидно, что описать движение прямой АВ в плоскости хОу можно посредством трех уравнений: первые два – описывают движение точки А (полюса), а последнее – угловое перемещение прямой АВ. Механически это можно объяснить следующим образом. Первые два уравнения описыва-
| ют поступательную составляющую движения тела, а последнее – вращательную.
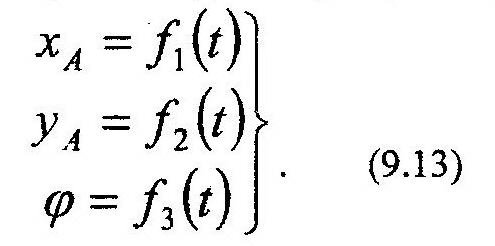 Действительно, сечение (S) тела (рис. 9.5) может перейти из положения А1В1 в положение А2В2 в два этапа. На первом этапе тело перемещается поступа-
Действительно, сечение (S) тела (рис. 9.5) может перейти из положения А1В1 в положение А2В2 в два этапа. На первом этапе тело перемещается поступа-
|
тельно; отрезок АВ занимает при этом промежуточное положение А2В’. На втором этапе происходит угловое перемещение (вращательное движение) всего сечения относительно неподвижной точки А2; при этом точка В и все сечение занимает свое окончательное положение. В действительности, при плоском движении совершается поступательное и
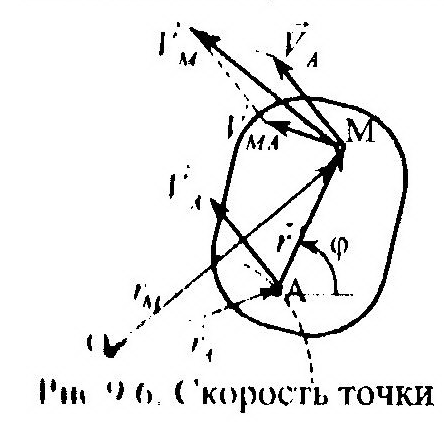
| вращательное движения одновременно. Однако, условное разделение геометрически сложного плоского движения тела на простые, позволяет предложить достаточно наглядный подход к определению скорости произвольной точки М тела (рис. 9.6). Использовав векторный способ определения положения точки, можно записать:

| |
| где | 
| - радиус-вектор точки М относительно точки А. |
Для определения скорости точки Мвозьмем производную по времени от левой и правой частей векторного выражения (9.14), получим:
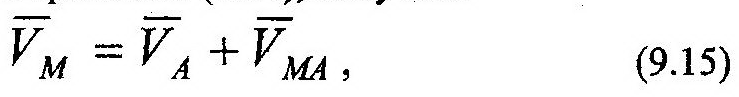
| где | 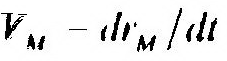
| - скорость точки М; |
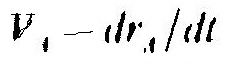
| - скорость полюса, точки А; | |

| - скорость точки Мотносительно полюса при угловом перемеще-нии тела. |
Таким образом,
скорость произвольной точки М тела при его плоском движении определяется как геометрическая сумма скорости другой какой-либо точки А, называемой полюсом, и скорости точки М, которую она получает при вращении тела вокруг полюса.
Однако, несмотря на свою достаточно ясную механическую сущность, выражение (9.15) оказывается непригодным для решения задач.
Другая зависимость между скоростями точек устанавливается
теоремой: проекции скоростей двух точек тела, совершающего плоское движение, на
Дата добавления: 2016-04-19; просмотров: 845;
