ВЫРАЖЕНИЕ ПОТЕНЦИАЛА ЛЮЛОЙ ТОЧКИ СХЕМЫ ЧЕРЕЗ ПОТЕНЦИАЛЫ СОСЕДНИХ ТОЧЕК

Рассмотрим на примере схемы рис. 1-15.

Рис. 1-15. Схема электрической цепи

Перед расчетом произвольно выбираются направления токов во всех ветвях и больше не меняются в процессе расчета.

Найдем разность потенциалов между точками d и n на пути ncabmd.

;

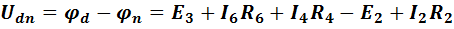. (1-18)

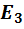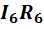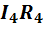При движении от точки n к точке c потенциал скачком возрастает на величину ЭДС . На участках ca и ab движемся против тока, т.е. в сторону возрастания потенциала, поэтому падения напряжения и входят в выражение (1-18) со знаком «плюс». Далее на участке bm скачок потенциала, поэтому падение напряжения входит в выражение (1-18) со знаком «плюс».

Разность потенциалов между точками d и n по кратчайшему пути будет:

U_dn = I₃R₃. (1-19)

Знак «плюс» соответствует возрастанию потенциала при движении от точки n к точке d по току.

Если при расчете по двум разным путям между одними и теми же точками получается одинаковая разность потенциалов, то можно считать, что токи рассчитаны верно. Это дополнительное средство проверки правильности расчета.

Найдем теперь разность потенциалов между точками b и m на пути mdncab:

U_bm = I₂R₂ – I₃R₃ + E₃ + I₆R₆ + I₄R₄; (1-20)

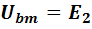. (1-21)