Данный момент времени равна нулю.

Можно показать, что в случае плоского движения тела такая точка существует и притом единственная. Для этого восстановим перпендикуляры из точек А и В (рис. 9.8) к соответствующим векторам скоростей V_A и V_B до их пересечения в точке Р (пересечение

состоится, т.к. векторы скоростей не параллельны). Предположим обратное, т.е. VP не равен 0. Тогда для каж-дой пары точек (А и Р) и (В и Р) должна выполняться теорема о проекциях скоростей на соответствующую прямую. Причем, выполняться теорема должна одновременно для указанных пар точек, что невозможно, т.к. вектор VP не может быть одновременно перпендикуля-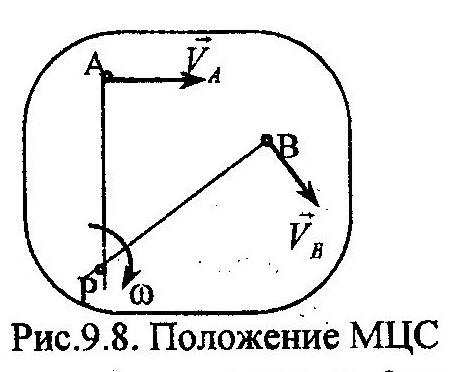

рен и прямой АР и прямой ВР. Теорема будет выполняться только в случае V_P=0. Это означает, что при нахождении МЦС достаточно найти точку, скорость которой в данный момент времени равна нулю. Со временем положение МЦС меняется и все новые точки сечения тела будут выполнять его функции. Практическое значение МЦС заключается в том, что с его помощью геометрически сложное плоское движение тела можно рассматривать как простое мгновенно вращательное движение относительно оси, проходящей через МЦС. Действительно, если в (9.15) в качестве полюса выбрать МЦС, скорость которой по определению равна нулю, то скорость произвольной точки М будет определяться по формуле:

а ее модуль:

т.е. скорость произвольной точки тела, совершающего плоское движение, опреляется как скорость, которую она получает при вращении тела вокруг МЦС.

На рис. 9.9 приведены случаи определения положения МЦС, отличные от общего правила, представленного на рис. 9.8. Поскольку для каждого момента времени существует един-

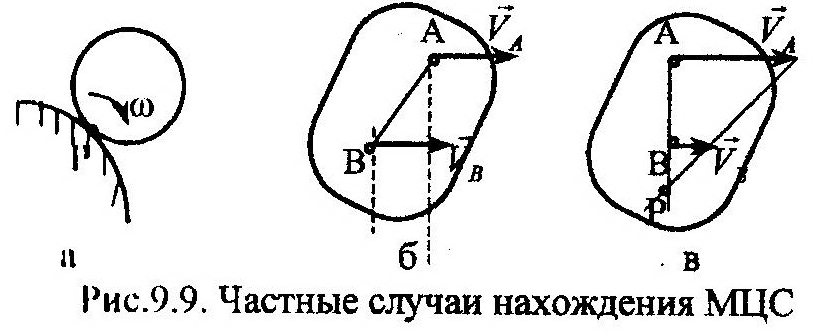
ственный МЦС, то в случае (а) этой точкой будет место касания диска неподвижной поверхности. В случае (б) перпендикуляры, восстановленные из точек А и В к скоростям, не пересекутся, т.к. векторы скоростей параллельны. Это

можно рассматривать как случай бесконечно удаленного МЦС, что на основе (9.20) приводит к равенству нулю угловой скорости и, как следствие, к выводу о поступательном характере движения тела. Случай (в) похож на предыдущий, но здесь перпендикуляры, восстановленные из точек А и В совпадают ниже точки В. Для определения положения МЦС необходимо построить дополнительную прямую, соединяющую кончики векторов скоростей и провести ее до пересечения с АВ. Точка пересечения и будет МЦС.