Всякое элементарное перемещение тела, имеющего одну неподвижную точку, можно представить как элементарный поворот относительно мгновенной оси вращения, проходящей через эту точку.
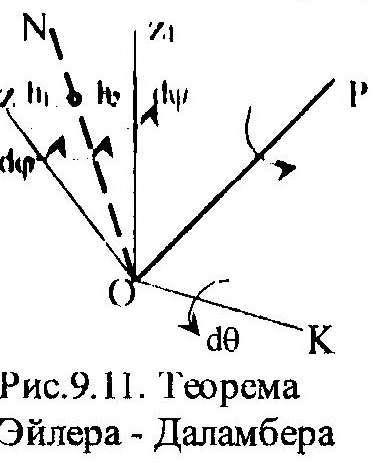
| Действительно, за время dt тело совершит элементарное перемещение, соответствующее изменению всех трех углов на величины dφ, dψ, dθ (рис. 9.11). Рассмотрим сначала вращение относительно осей Оz и Оz1. В плоскости zОz1 всегда можно найти такую точку, отсто-ящую от осей z и z1 на расстояния h1 и h2, суммарное пе-ремещение которой равно нулю, т.е. h1dφ+h2 dψ=0. Имея две неподвижные точки, можно рассматривать перемещение тела как элементарный поворот относи- |
сительно мгновенной оси вращения ON. Рассуждая подобным образом, можно найти точку в плоскости NOK, суммарное перемещение которой равно нулю. При этом элементарном перемещении тела произойдет изменение всех трех углов, определяющих его положение в пространстве. Таким образом, элементарный поворот тела с одной неподвижной точкой можно представить как элементарное вращательное движение относительно мгновенной оси ОР, проходящей через эту же точку, что и требовалось доказать.
Основные кинематические характеристики движения тела:
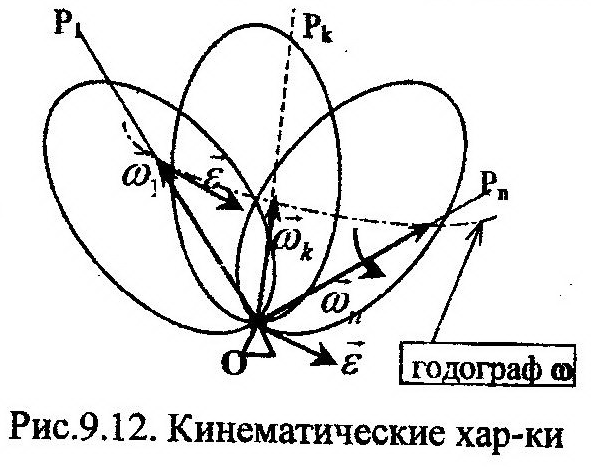
1. Угловая скорость ω, с которой тело совершает элементарный поворот относительно мгновенной оси вращения ОР. Вектор угловой скорости направлен по этой оси (рис. 9.12). Поскольку ось со временем меняет свое положение в пространстве, постольку и вектор ω
в каждый момент времени имеет новую ориентацию. Кривая, которую описывает вектор ω в пространстве, называется годографом ω.
2. Угловое ускорение ε – величина, характеризующая изменение угловой скорости:
 Чтобы представить ориентацию вектора ε впрост-ранстве, сравним (9.22) с выражением скорости точки,
Чтобы представить ориентацию вектора ε впрост-ранстве, сравним (9.22) с выражением скорости точки,
| 
| |
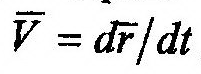
| . Здесь прослеживается прямая аналогия. | |
Учитывая, что вектор V направлен по касательной к годографу радиуса-вектора, r, в векторном способе задания движения точки, можно предположить, что и вектор ускорения будет направлен по касательной к годографу угловой скорости (рис. 9.12).
Основные кинематические характеристики движения точки тела:
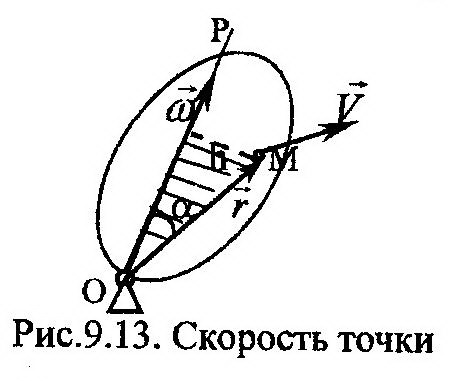
1. Скорость точки, V.Поскольку мгновенная ось вращения ОР меняет свое положение в пространстве, то использовать формулу скорости точки (9.10) при вращательном движении тела практически невозможно. Представляет интерес следующая формула:
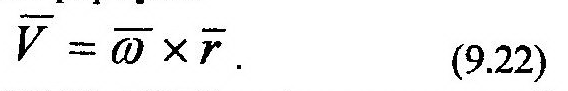 Действительно, модуль вектора, который получается в ре-зультате векторного произведения ω на r, соответствую-щий точке где определяется скорость, равен:
Действительно, модуль вектора, который получается в ре-зультате векторного произведения ω на r, соответствую-щий точке где определяется скорость, равен:
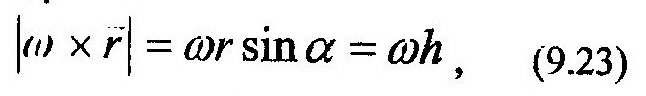
| 
|
что соответствует скорости точки, определяемой по формуле (9.10).
Направление V нормально плоскости, задаваемой векторами ω и r.
2. Ускорение точки, а, можно определить как производную по времени от вектора скорости:
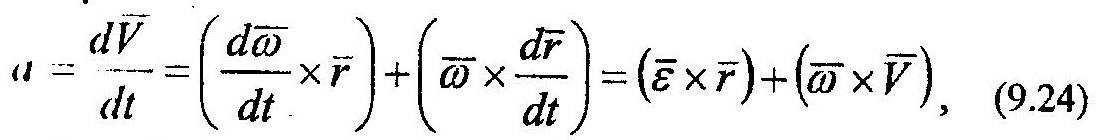
Дата добавления: 2016-04-19; просмотров: 912;
