Плоскость и прямая в пространстве. Поверхности второго порядка.

Плоскость.

Рассмотрим в декартовом базисе произвольную плоскость Р и вектор нормали (перпендикулярный) к ней `n (А, В, С). Возьмем в этой плоскости произвольную фиксированную точку М<sub>0</sub>(х<sub>0</sub>, у<sub>0</sub>, z<sub>0</sub>) и текущую точку М(х, у, z). Очевидно, что 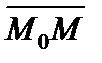×`n = 0 (1.53)

(см.(1.20) при j = p /2). Это уравнение плоскости в векторной форме. Переходя к координатам, получим общее уравнение плоскости

А(х – х₀) + В(у – у₀) + С(z – z₀) = 0 ÞАх + Ву + Сz + D = 0 (1.54).

(D = –Ах₀– Ву₀ – Сz₀; А² + В² + С² ¹ 0).

Можно показать, что в декартовых координатах каждая плоскость определяется уравнением первой степени и, обратно, каждое уравнение первой степени определяет плоскость, (т.е. плоскость есть поверхность первого порядка и поверхность первого порядка есть плоскость).

Рассмотрим некоторые частные случаи расположения плоскости, заданной общим уравнением:

А = 0 – параллельна оси Ох; В = 0 – параллельна оси Оу; С = 0 – параллельна оси Оz. (Такие плоскости, перпендикулярные одной из координатных плоскостей, называют проектирующими); D = 0 – проходит через начало координат; А = В = 0 – перпендикулярна оси Оz (параллельна плоскости хОу); А = В = D = 0 – совпадает с плоскостью хОу (z = 0). Аналогично анализируются все остальные случаи.

Если D ¹ 0, то, разделив обе части (1.54) на -D, можно привести уравнение плоскости к виду: 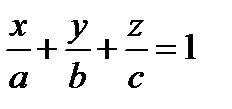(1.55),

а = – D /А, b = –D/ В, с =–D /С. Соотношение (1.55) называетcя уравнением плоскости в отрезках; а, b, с – абсцисса, ордината и аппликата точек пересечения плоскости с осями Ох, Оу, Оz, а |a|, |b|, |c| – длины отрезков, отсекаемых плоскостью на соответствующих осях от начала координат.

Умножая обе части (1.54) на нормирующий множитель 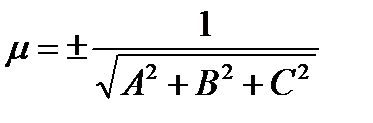(mD < 0) получим нормальное уравнение плоскости:

xcosa + ycosb + zcosg – p = 0 (1.56)

где cosa = Аm, cosb = Вm, cosg = Сm – направляющие косинусы нормали к плоскости, р – расстояние до плоскости от начала координат.

Рассмотрим основные соотношения, используемые в расчетах. Угол между плоскостями А₁х + В₁у + С₁z + D₁ = 0 и А₂х + В₂у + С₂z + D₂ = 0 легко определить как угол между нормалями этих плоскостей `n₁ (А₁, В₁, С₁)и

`n₂ (А₂, В₂, С₂): 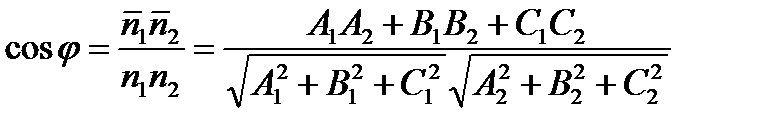(1.57)

Из (1.57) легко получить условие перпендикулярности

А₁А₂ + В₁ В₂ + С₁ С₂ = 0 (1.58)

и параллельности 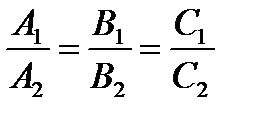(1.59) плоскостей и их нормалей.

Расстояние от произвольной точки М₀(х₀, у₀, z₀) до плоскости (1.54)

определяется выражением: 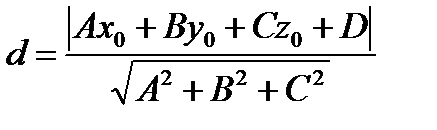(1.60)

Уравнение плоскости, проходящей через три заданные точки М₁(х₁, у₁, z₁), М₂(х₂, у₂, z₂), М₃(х₃, у₃, z₃) удобнее всего записать используя условие компланарности (1.25) векторов 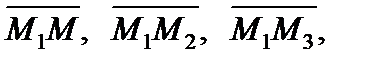гдеМ(х, у, z) – текущая точка плоскости.

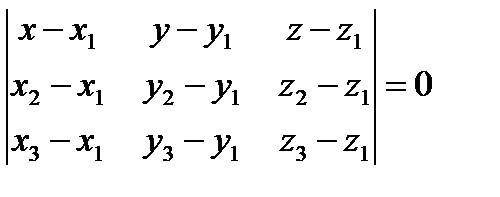(1.61)

Приведем уравнение пучка плоскостей (т.е. множества плоскостей, проходящих через одну прямую) – его удобно использовать в ряде задач.

(А₁х + В₁у + С₁z + D₁) + l(А₂х + В₂у + С₂z + D₂) = 0 (1.62)

Где l Î R, а в скобках - уравнениядвух любых плоскостей пучка.

Контрольные вопросы.

1) Как проверить, что данная точка лежит на поверхности, заданной данным уравнением?

2) Каков характерный признак, отличающий уравнение плоскости в декартовой системе координат от уравнения других поверхностей?

3) Как расположена плоскость относительно системы координат, если в её уравнении отсутствует: а) свободный член; б) одна из координат; в) две координаты; г) одна из координат и свободный член; д) две координаты и свободный член?

Тест 11.

1) Даны точки М₁(0,-1,3) и М₂(1,3,5). Написать уравнение плоскости, проходящей через точку М₁ и перпендикулярной к вектору 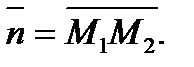Выбрать верный ответ:

а) 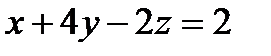; б) .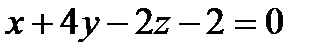

2) Найти угол между плоскостям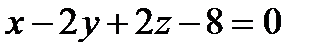и и 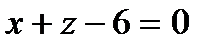. Выбрать верный ответ:

а) 135^о, б) 45^о

1.7.2. Прямая.Плоскости, нормали которых не коллинеарны, 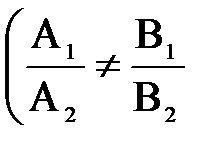или 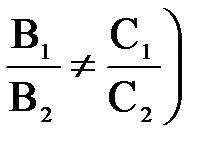пересекаются, однозначно определяя прямую как линию их пересечения, что и записывается следующим образом:

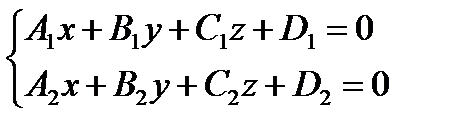(1.63)

Через эту прямую можно провести бесконечно много плоскостей (пучок плоскостей (1.62)), в том числе и проектирующие ее на координатные плоскости. Чтобы получить их уравнения, достаточно преобразовать (1.63), исключив из каждого уравнения по одной неизвестной и приведя их, например, к виду 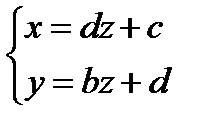(1.63`).

Поставим задачу – провести через точку М₀(х₀,у₀,z₀) прямую, параллельную вектору `S (l, m, n) (его называют направляющим). Возьмем на искомой прямой произвольную точку М(х,у,z). Векторы 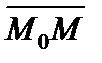и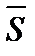должны быть коллинеарны, откуда получаем канонические уравнения прямой.

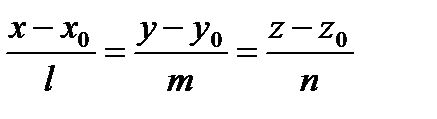(1.64) или 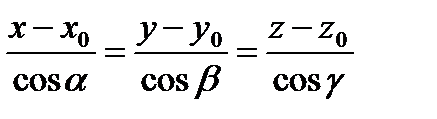(1.64`)

где cosa, cosb, cosg – направляющие косинусы вектора `S. Из (1.64) легко получить уравнение прямой, проходящей через заданные точки М₁(х₁, у₁, z₁) и М₂(х₂, у₂, z₂) (она параллельна )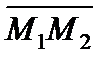

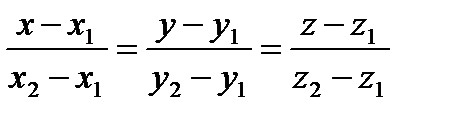или 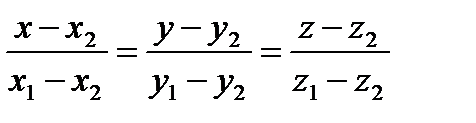(1.64``)

(Значения дробей в (1.64) равны для каждой точки прямой и могут быть обозначены через t, где t 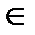R. Это позволяет ввести параметрические уравнения прямой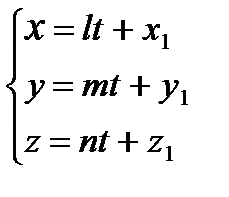

Каждому значению параметра tсоответствует набор координат х, у, z точки на прямой или (иначе) - значения неизвестных, удовлетворяющих уравнениям прямой).

Используя уже известные свойства векторов и операций над ними и канонические уравнения прямой легко получить следующие формулы:

Угол между прямыми: 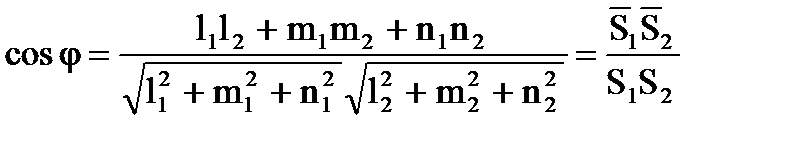(1.65)

где `S<sub>1</sub> и `S₂ – направляющие векторы прямых.

Условие параллельности 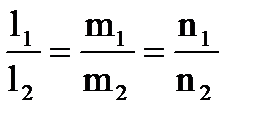(1.66).

перпендикулярности l₁l₂ + m₁m₂ + n₁n₂ = 0(1.67) прямых.

Угол между прямой и плоскостью (легко получить, найдя угол между прямой и нормалью к плоскости, составляющий в сумме с искомым p/2)

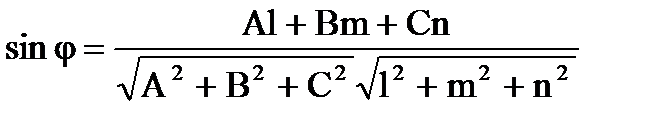(1.68)

Из (1.66) получаем условие параллельности Al + Bm + Cn = 0 (1.69)

и перпендикулярности 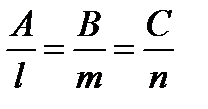(1.70) прямой и плоскости. Необходимое и достаточное условие нахождения двух прямых в одной плоскости легко получить из условия компланарности (1.25).

(1.71)

контрольные вопросы.

1) Каковы способы задания прямой линии в пространстве?

Тест 12.

1) Написать уравнения прямой, проходящей через точку А(4,3,0) и параллельной вектору 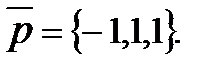Указать верный ответ:

а) 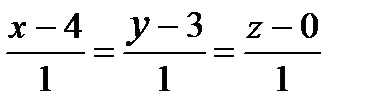; б) .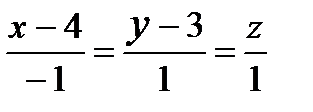

2) Написать уравнения прямой, проходящей через точки А(2,-1,3) и В(2,3,3). Указать верный ответ.

а) 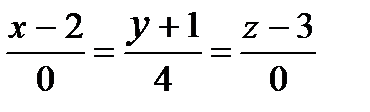; б) .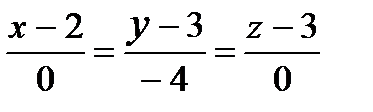

3) Найти точку пересечения прямой с плоскостью: 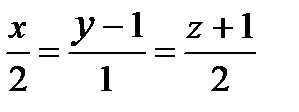, 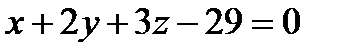. Указать верный ответ:

а) (6,4,5); б) (6,-4,5).

1.7.3. Поверхности второго порядка. Если линейное уравнение в трехмерном декартовом базисе однозначно определяет плоскость, любое нелинейное уравнение, содержащее х, у, z описывает какую – то иную поверхность. Если уравнение имеет вид

Ах² + Ву² + Cz² + 2Dxy + 2Exz + 2Fyz + 2Gx + 2Hy + 2Kz + L = 0,то оно описывает поверхность второго порядка (общее уравнение поверхности второго порядка). Выбором или преобразованием декартовых координат уравнение можно максимально упростить, приведя к одной из следующих форм, описывающих соответствующую поверхность.

1. Канонические уравнения цилиндров второго порядка, образующие которых параллельны оси Oz, а направляющими служат соответствующие кривые второго порядка, лежащие в плоскости хОу:

(1.72), 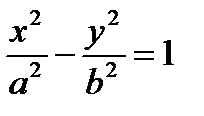(1.73), у² = 2рх (1.74)

эллиптический, гиперболический и параболический цилиндры соответственно.

(Напомним, что цилиндрической называют поверхность, полученную перемещением прямой, называемой образующей, параллельно самой себе. Линию пересечения этой поверхности с плоскостью, перпендикулярной образующей, называют направляющей – она определяет форму поверхности).

По аналогии можно записать уравнения таких же цилиндрических поверхностей с образующими, параллельными оси Оу и оси Oх. Направляющую можно задать, как линию пересечения поверхности цилиндра и соответствующей координатной плоскости, т.е. системой уравнений вида:

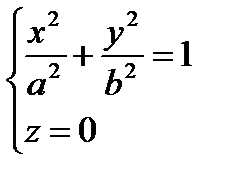
2. Уравнения конуса второго порядка с вершиной в начале координат:

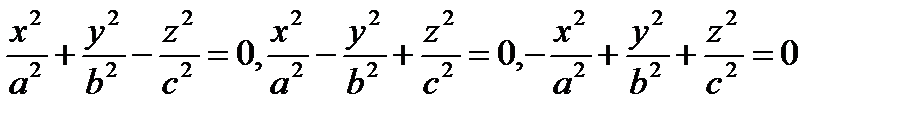(1.75)

(осями конуса служат оси Oz, Oy и Ох соответственно)

3. Каноническое уравнение эллипсоида: (1.76);

Частными случаями являются эллипсоиды вращения, например 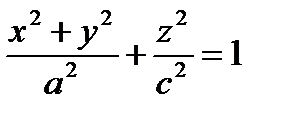– поверхность, полученная вращением эллипса вокруг оси Оz (При

а > с эллипсоид сжат, при a < c – удлинен) и сфера (при а = b = с = r получим

х² + у²+ z² + = r² – уравнение сферы радиусаrс центром в начале координат).

4. Каноническое уравнение однополостногогиперболоида

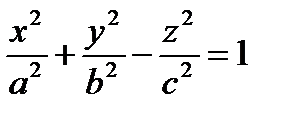(1.77)

(знак “ – ” может стоять перед любым из трех слагаемых левой части – это изменяет только положение поверхности в пространстве). Частные случаи – однополостные гиперболоиды вращения, например 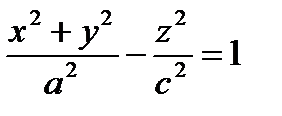– поверхность, полученная вращением гиперболы вокруг осиOz (мнимой оси гиперболы).

5. Каноническое уравнение двухполостного гиперболоида

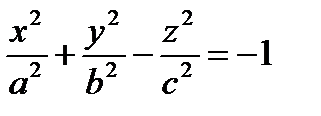(1.78)

(знак “ – ” может стоять перед любым из трех слагаемых левой части).

Частные случаи – двухполостные гиперболоиды вращения, например 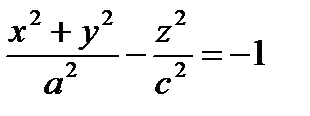– поверхность, полученная вращением гиперболы вокруг оси Оz (действительной оси гиперболы).

6. Каноническое уравнение эллиптического параболоида

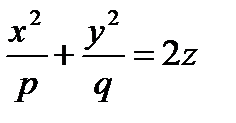(p >0, q >0) (1.79)

(переменная z может поменяться местами с любой из переменных х и у – изменится положение поверхности в пространстве).

7. Каноническое уравнение гиперболического параболоида

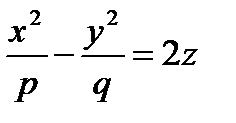(p >0, q >0) (1.80)

(переменная z может поменяться местами с любой из переменных х и у– изменится положение поверхности в пространстве).

Отметим, что представление об особенностях (форме) этих поверхностей легко получить, рассматривая сечения этих поверхностей плоскостями, перпендикулярными осям координат.

контрольные вопросы.

1) Какое множество точек в пространстве определяет уравнение ?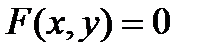

2) Каковы канонические уравнения цилиндров второго порядка; конуса второго порядка; эллипсоида; однополостного гиперболоида; двухполостного гиперболоида; эллиптического параболоида; гиперболического параболоида?

Тест 13.

1) Найти центр и радиус сферы 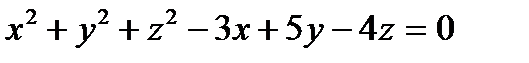и указать верный ответ:

а) С(1,5;-2,5;2), 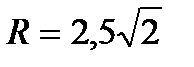; б) С(1,5;2,5;2), ;

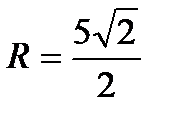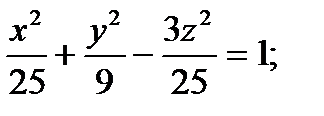
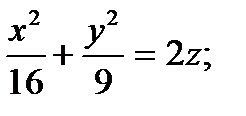
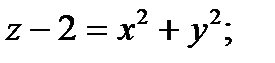
2) Определить вид поверхности, заданной уравнениями: 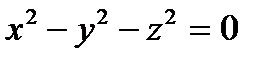. Указать верный ответ:

а) однополостный гиперболоид; гиперболический параболоид; эллиптический параболоид; конус.

б) двухполостный гиперболоид; гиперболический параболоид; эллиптический параболоид; конус.