В скомпенсированных полупроводниках

Часто в приборах встречаются кристаллы полупроводников (или области в кристалле) легированные как донорами, так и акцепторами. Такие полупроводники называют скомпенсированными. Расчет положения уровня Ферми для полностью компенсированного полупроводника, т.е. полупроводника с равными концентрациями доноров и акцепторов ( 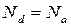) и частично компенсированного полупроводника ( ) с учетом уравнения электронейтральности рассмотрен в лекционном курсе. Электроны, попавшие в зону проводимости с доноров, уходят из нее преимущественно на акцепторные уровни, как энергетически более низкие (рис. 1.5).

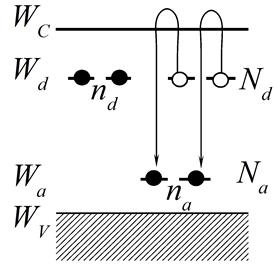
Рис. 1.5. Зонная схема частично компенсированного полупроводника n-типа

При этот процесс приведет к тому, что все донорные центры окажутся пустыми, а все акцепторные – занятыми электронами, т.е. 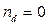и 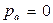. Уровень Ферми в полностью компенсированном полупроводнике, как и в собственном, лежит вблизи середины запрещенной зоны (формула 1.6). Концентрация носителей заряда в нем определяется генерацией собственных носителей. Проводимость полностью скомпенсированного полупроводника может быть ниже, чем собственного, из-за рассеяния энергии носителей заряда на дефектах кристалла (донорных и акцепторных примесях) и снижения подвижностей.

Для частично скомпенсированного полупроводника при N_d = 2N_a при
Т = 0 уровень Ферми совпадает с донорными уровнями.

Таким образом, уровень Ферми сохраняет в широком интервале концентраций свое положение вблизи 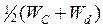для полупроводников
n-типа и вблизи 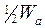для полупроводников р-типа. Около N_d = N_a его положение резко меняется (рис. 1.6).

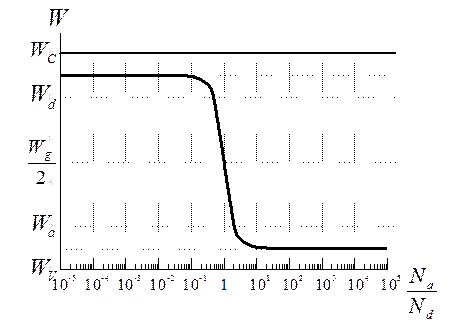
Рис. 1.6. Зависимость положения уровня Ферми от соотношения концентраций акцепторов и доноров

В случае, когда разница между концентрациями доноров и акцепторов составляет более порядка можно проводить расчет концентраций носителей как для примесного полупроводника с одной примесью, а концентрацию примеси считать как N_d – N_a для полупроводника n-типа и N_a – N_d для полупроводника
p-типа.

Анализ более сложных полупроводниковых систем с многозарядными центрами выходит за рамки нашего курса.

ЗАДАЧА 1.4

Рассчитайте концентрации носителей заряда при 300 и 520 К в частично скомпенсированном полупроводнике с шириной запрещенной зоны 0,9 эВ. Донорная примесьвведена в концентрации 2×10¹⁴ см^-3, энергетический зазор между дном зоны проводимости и уровнями доноров составляет 0,01 эВ. Акцепторная примесьвведена в концентрации 6×10¹⁴ см^-3, энергетический зазор между потолком валентной зоны и уровнями акцепторов составляет 0,03 эВ. Эффективные массы – = 0,5 m; = 0,4 m.

Дано:

Полупроводник частично скомпенсированный:

Запрещенная зона – W_g =0,9 эВ;

Примесь донорная: W_d = 0,01 эВ, N_d = 2×10¹⁴ см^-3;

Примесь акцепторная: W_а = 0,02 эВ, N_a = 6×10¹⁴ см^-3;

Эффективные массы – = 0,5 m; = 0,4 m;

Температуры T₁= 300 K, T₂= 520 K.

Найти:

n, p.

Решение:

1) При 300 К

Область истощения доноров наступит при 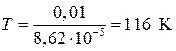, а акцепторов при 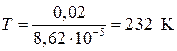, т.е. при 300 К примеси могут быть полностью ионизированы. Электроны, попавшие в зону проводимости с донорных уровней, уходят из нее преимущественно на акцепторные уровни и занимают их. Таким образом, акцепторы окажутся занятыми, а проводимость будет электронной.

Чтобы определить, наступает ли при этой температуре область собственной проводимости, найдем концентрацию собственных носителей заряда:

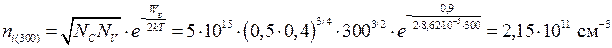Т.е. 300 К относится к области насыщения. Электронами будет занята часть акцепторов, остальная часть акцепторов (N_a – N_d = 4×10¹⁴ см^-3) будет полностью ионизирована. Концентрация дырок p₍₃₀₀₎= 4×10¹⁴ см^-3, концентрация электронов равна:

.

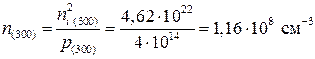3) При 520 К.

Найдем концентрацию собственных носителей заряда:

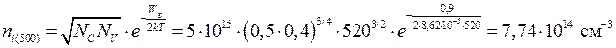Т.е. 500 К относится к смешанной области. Электронами будет занята та же часть акцепторов. Концентрацию дырок найдем по (1.18):

.

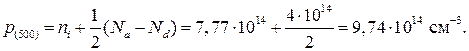
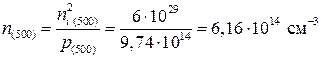Ответ:

Концентрации носителей составляют:

n₍₃₀₀₎= 1,16^.10⁸ см^-3, р₍₃₀₀₎ = 4·10¹⁴см^-3;

n₍₅₀₀₎= 6,16^.10¹⁴ см^-3, р₍₅₀₀₎ = 9,74·10¹⁴см^-3.