Определение концентрации носителей тока в собственных полупроводниках
Определение равновесной концентрации носителей тока в полупроводниках
Общие сведения
Важность определения концентрации носителей заряда (т.е. свободных электронов и дырок) в полупроводнике связано с тем, что эта концентрация определяет одно из важнейших свойств полупроводника – его электропроводность.
Если проводник находится вне воздействия внешних электромагнитных полей и излучений, то ионы и электроны в нем находятся в равновесном состоянии. Согласно статистике Ферми – Дирака, оно характеризуется вполне определенным распределением электронов по разрешенным энергетическим уровням полупроводника.
Статистика Ферми – Дирака учитывает неразличимость (или «тождественность») частиц, и описывает системы частиц с полуцелым спином, т.е. системы электронов, протонов и нейтронов. Функция распределения Ферми – Дирака в общем виде имеет вид:
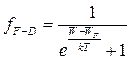 (1.1)
(1.1)
где W – заданная энергия; f – вероятность заполнения частицами уровня с энергией W; k – постоянная Больцмана; T – заданная температура;
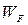 – энергетический параметр (энергия Ферми).
– энергетический параметр (энергия Ферми).
Таким образом, значение функции Ферми – Дирака зависит от положения WF относительно энергетических уровней системы и температуры.
Функция Ферми – Дирака из-за наличия в знаменателе слагаемого – единицы, неудобна в аналитических (не численных) расчетах. Но ее можно аппроксимировать более удобной для расчетов функцией. При 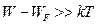 первое слагаемое в знаменателе становится существенно больше единицы. Это позволяет пренебречь единицей и записать:
первое слагаемое в знаменателе становится существенно больше единицы. Это позволяет пренебречь единицей и записать:
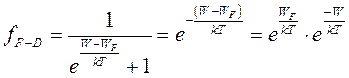 (1.2)
(1.2)
Первый сомножитель является константой для каждого материала, обозначим ее A. Тогда:
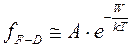 , (1.3)
, (1.3)
т.е. распределение Ферми – Дирака принимает вид распределения Максвелла –Больцмана. Соответствие обеих функций становится удовлетворительным при условии 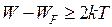 . Это условие выполняется в ряде практически важных расчетов, в том числе и при решении задач. При W>>WF аппроксимирующая функция для электронов имеет вид:
. Это условие выполняется в ряде практически важных расчетов, в том числе и при решении задач. При W>>WF аппроксимирующая функция для электронов имеет вид:
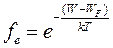 (1.4)
(1.4)
Аналогично, при условии W<<WF, и при учете того, что для дырок вероятность заполнения энергетических уровней обратная fh = 1 – fe, функция (1.2) примет вид:
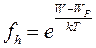 (1.5)
(1.5)
Выражение (1.4) используют при расчете концентрации электронов, а выражение (1.5) – для расчета концентрации дырок.
Определение концентрации носителей тока в собственных полупроводниках
Собственным полупроводником называют полупроводник, в котором нет дополнительных уровней в запрещенной зоне, и генерация носителей заряда в нем может происходить только при переходе электрона из валентной зоны в зону проводимости (рис. 1.1).
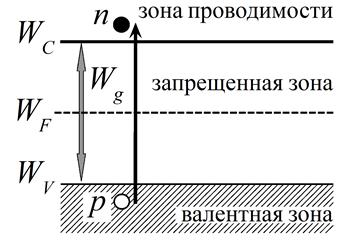
| Рис. 1.1. Зонная схема собственного полупроводника и генерация носителей заряда в нем |
В самом простом случае можно сказать, что это полупроводник без примесей. Однако создавать уровни в запрещенной зоне могут не только специально введенные примеси, но и дефекты нестехиометрии в бинарных (и более сложных) полупроводниках, а также и другие точечные дефекты монокристаллов полупроводников. Чистые однокомпонентные полупроводники можно считать собственными. В них из-за механизма генерации носителей концентрации свободных электронов и дырок всегда будут равны n = p.
Расчеты показывают (рассмотрены в лекционном курсе), что уровень Ферми в собственном полупроводнике лежит вблизи середины запрещенной зоны. Положение уровня Ферми определяется формулой:
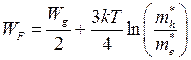 (1.6)
(1.6)
При T=0 второе слагаемое равно нулю, и энергия уровня Ферми равна половине ширины запрещенной зоны. Для реальных значений T, 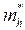 и
и 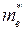 второе слагаемое не равно нулю, но обычно составляет малую долю от величины первого слагаемого (подробнее в задаче 1.7), и поэтому приближенно можно считать, что уровень Ферми собственного полупроводника расположен в середине запрещенной зоны. Таким образом, для собственного полупроводника:
второе слагаемое не равно нулю, но обычно составляет малую долю от величины первого слагаемого (подробнее в задаче 1.7), и поэтому приближенно можно считать, что уровень Ферми собственного полупроводника расположен в середине запрещенной зоны. Таким образом, для собственного полупроводника:
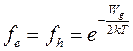 . (1.7)
. (1.7)
ЗАДАЧА 1.1
В собственном полупроводнике ширина запрещенной зоны 0,8 эВ. Эффективная масса электрона в зоне проводимости равна 0,56 m,а дырки–
0,37 m. Подвижность электронов при 300 К равна 3800 см2·В-1·с-1 и зависит от температуры по следующему закону μe = а·Т-3/2 (параметр а принять неизменным). Подвижность дырок в области исследуемых температур меньше подвижности электронов в 2 раза. Нужно найти концентрации свободных электронов и дырок при 27 оС, 80 оС и 180 оС, построить график зависимости концентрации свободных электронов от температуры, определить проводимость полупроводника при этих температурах.
Дано:
Полупроводник собственный:
Запрещенная зона – Wg =0,8 эВ;
Эффективные массы –  = 0,56 m;
= 0,56 m;  = 0,37 m;
= 0,37 m;
Подвижности μе = 3800 см2·В-1·с-1;
μe= а·Т-3/2 (а = const);
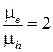 .
.
Температуры t1=27 оС, t2 = 80 оС, t3 =180 оС.
Найти:
n, p; σ.
Решение:
Концентрации свободных электронов и дырок в собственном полупроводнике равны n = p = ni, поэтому мы будем проводить расчет только для электронов. Концентрация электронов в зоне проводимости равна произведению эффективной плотности состояний в этой зоне и функции распределения:
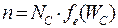 . (1.8)
. (1.8)
Эффективные плотности состояний (см-3) равны:
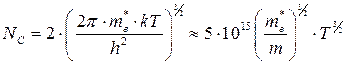 (1.9)
(1.9)
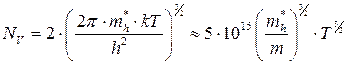 (1.10)
(1.10)
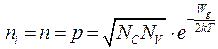 (1.11)
(1.11)
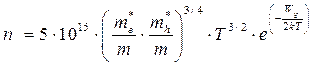 (1.12)
(1.12)
Во всех расчетах необходимо использовать значения температур по термодинамической шкале (т.е. в К). Таким образом, при 27 оС (300 К) концентрация электронов в зоне проводимости равна:
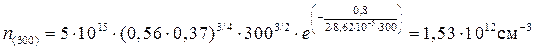 .
.
При 80 оС (353 К) – равна:
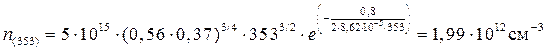 .
.
При 180 оС (453 К) – равна:
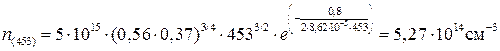 .
.
Концентрация электронов в зоне проводимости с температурой растет экспоненциально, поэтому график зависимости удобно представлять в арениусовских координатах (концентрацию – по логарифмической шкале, а температуру в виде  ). Занесем в таблицу (табл. 1.1) значения температуры и концентрации носителей заряда, а затем построим график (рис. 1.2).
). Занесем в таблицу (табл. 1.1) значения температуры и концентрации носителей заряда, а затем построим график (рис. 1.2).
Таблица 1.1
Зависимость концентрации свободных электронов от температуры в собственном полупроводнике
| 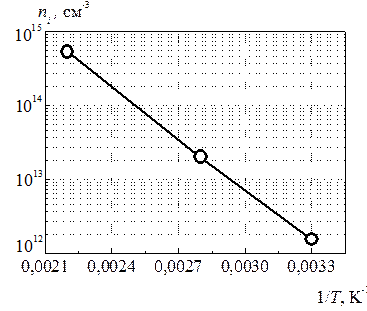 Рис. 1.2. Зависимость концентрации собственных носителей тока от температуры
Рис. 1.2. Зависимость концентрации собственных носителей тока от температуры
|
Найдем значения подвижностей (см2·В-1·с-1·K3/2):
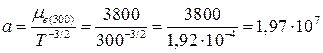 .
.
Таким образом:
µe(353) = a·Т-3/2 = 1,97·107·353-3/2 = 2977;
µe(453) = a·Т-3/2 = 1,97·107·453-3/2 = 2048;
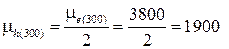 ;
;
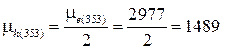 ;
;
 .
.
Найдем величины электропроводности. В общем случае электропроводность равна:
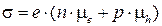 , (1.13)
, (1.13)
где е – заряд электрона 1,6·10-19 Кл.
Для собственного проводника: 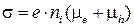 .(1.14)
.(1.14)
Таким образом, значения проводимостей (Ом-1·см-1):
σ(300) = 1,6·10-19·1,53.1012· (3800 + 1900) = 1,40·10-3;
σ(353) = 1,6·10-19·1,99.1013· (2977 + 1489) = 1,42·10-2;
σ(453) = 1,6·10-19·5,27.1014· (2048 + 1024) = 0,26.
Ответ:
Концентрации собственных носителей составляют:
при 27 оС 1,53.1012 см-3, при 80 оС 1,99.1013см-3, при 180 оС 5,27.1014 см-3.
Удельная электропроводность полупроводника составляет:
при 27 оС 1,40·10-3 Ом-1·см-1, при 80 оС 1,42·10-2 Ом-1·см-1,
при 180 оС 0,26 Ом-1·см-1.
Дата добавления: 2016-02-16; просмотров: 4091;
