Частные случаи задач определения концентрации носителей тока
Часто в задачах указывается конкретный материал полупроводника. В таких случаях можно пользоваться известными данными про ширину запрещенной зоны, эффективные массы и подвижности.
Для расчета концентрации собственных носителей заряда в самых широко применяемых полупроводниках – кремнии и германии – в практических расчетах можно использовать следующее выражение, выведенное из (1.11):
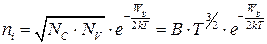 , (1.19)
, (1.19)
где В – константа, учитывающая эффективные массы носителей заряда. Значения константы В, ширины запрещенной зоны, типичные значения подвижностей, а также некоторых других свойств представлены в табл. 1.3.
Таблица 1.3
Константы для расчета концентраций носителей
| Свойство | Полупроводник | |
| Si | Ge | |
| B, K-3/2·см-3 | 3,87×1016 | 1,76×1016 |
| Wg, эВ | 1,21 | 0,785 |
| μе*,см2·В-1·с-1 | ||
| μh*, см2·В-1·с-1 | ||
| Относительная диэлектрическая проницаемость, ε | ||
| Молярная масса, М, г/моль | 28,08 | 72,61 |
| Плотность, ρ, г/см3 | 2,33 | 5,32 |
| Концентрация собственных носителей заряда при 300 K, ni(300), см-3 | 1,4·1010 | 2,3·1013 |
* Подвижность носителей заряда зависит от температуры, уровня легирования, качества кристалла, но для задач, где нет других данных, можно использовать эти данные.
ЗАДАЧА 1.5
Какова должна быть концентрация донорной примеси в кремнии, чтобы его проводимость при 300 К была равна проводимости чистого германия?
Дано:
Полупроводник №1 (Ge) собственный:
Запрещенная зона – Wg =0,785эВ;
Подвижности μе(Ge) = 3900 см2·В-1·с-1;
μh(Ge) = 1900 см2·В-1·с-1;
Температура T = 300 K;
Полупроводник №2 (Si) примесный (n-типа):
Запрещенная зона – Wg =1,21эВ;
Подвижности μе(Ge) = 1200 см2·В-1·с-1;
μh(Ge) = 500 см2·В-1·с-1;
Температура T = 300 K;
σ(Ge) = σ(n-Si).
Найти:
Nd
Решение:
Приравняем проводимости наших полупроводников (1.13, 1.14):
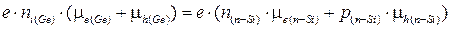 (1.20)
(1.20)
Так как нам известно, что наши полупроводники – германий и кремний, то можем записать для них:
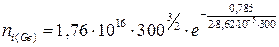 =2,3·1013 см-3;
=2,3·1013 см-3;
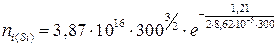 =1,4·1010 см-3.
=1,4·1010 см-3.
Из-за меньшей ширины запрещенной зоны концентрация собственных носителей тока при одинаковой температуре в германии будет на порядки выше, чем в кремнии. Обозначим концентрацию электронов в зоне проводимости кремния, легированного донорами n(n-Si), тогда концентрация дырок в нем будет равна:
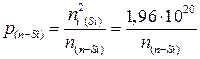
Подставим все известные значения в (1.20) и получим:
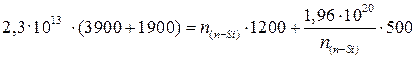 ;
;
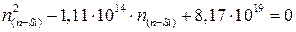
Это обычное квадратное уравнение, найдем его корни:
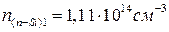 и
и 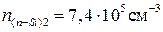 .
.
Второй корень не подходит, так как концентрация электронов в зоне проводимости в полупроводнике n-типа не может быть меньше ni. Таким образом, концентрация электронов 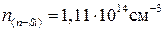 .
.
Рассчитаем, в какую область попадает 300 K, для чего найдем NC(Si). Для этого подставим в (1.9) значения (1.19):
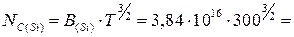 2,00×1020 см-3
2,00×1020 см-3
Получаем: ni=1,4·1010 см-3, NC = 2,00×1020 см-3, т.е. ni<<NC, т.е. попадаем в область (1.17):
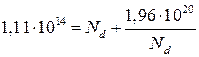 ;
;
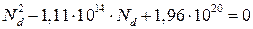
Опять получили квадратное уравнение, корни которого 1,8·106 и 1,11·1015. Первый корень не подходит, так как такая концентрация не отвечает условию (1.17). Таким образом, концентрация доноров 1,11·1014 см-3.
Ответ:
Концентрация доноров 1,11·1014 см-3.
ЗАДАЧА 1.6
На сколько нужно повысить температуру чистого германия с 300 К, чтобы концентрация электронов увеличилась в 2 раза.
Дано:
Полупроводник (Ge) собственный:
Запрещенная зона – Wg =0,785эВ;
Температура T = 300 K;
Концентрации носителей тока, n(Т1) =2n(300);
Найти:
T1
Решение:
Так как нам известно, что наш полупроводник – германий, то можем воспользоваться формулой (1.19) и записать для обеих температур:
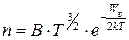 ,
,
при этом, n(Т1) =2n(300), поэтому:
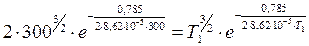 ;
;
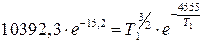 ;
;
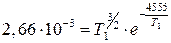 .
.
Такое уравнение аналитически решить трудно, поэтому можно решать его численными методами (в любой компьютерной программе, например MS Excel), если это по каким-то причинам затруднительно, то можно решить уравнение графически или построить график зависимости концентрации носителей заряда от температуры по формуле (1.19). Из задачи 1.1 мы знаем, что в собственном полупроводнике концентрация носителей с температурой растет экспоненциально, т.е. в два раза вырастает при небольшом увеличении температуры. Рассчитаем концентрацию носителей при трех температурах – 300, 310 и 320 К.
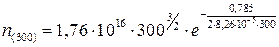 =2,34·1013см-3.
=2,34·1013см-3.
Нам нужно найти температуру, при которой n=2·n(300) = 4,68·1013 см-3
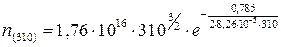 =4,01·1013см-3;
=4,01·1013см-3;
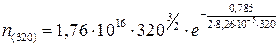 =6,66·1013см-3.
=6,66·1013см-3.
Искомая температура лежит между 310 и 320 К. Нанесем точки (табл. 1.4) на график (рис. 1.5).

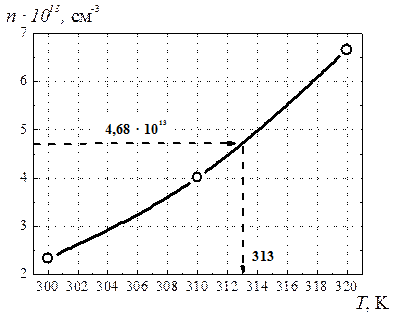 Рис. 1.5. Зависимость концентрации электронов
Рис. 1.5. Зависимость концентрации электронов
в зоне проводимости от температуры
Таким образом, искомая температура 313 К.
Ответ:
Температуру нужно поднять на 13 градусов.
ЗАДАЧА 1.7
В чистом антимониде индия InSb при 300 К эффективная масса дырок больше эффективной массы электронов в 100 раз. Как изменится положение уровня Ферми при нагревании от комнатной температуры до 80 оС? Принять отношение эффективных масс неизменным во всем в исследуемом диапазоне температур.
Дано:
Полупроводник (InSb) собственный:
Эффективные массы – 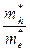 = 100;
= 100;
Температуры t1=20 оС, t2 = 80 оС.
Найти:
Изменение положения уровня Ферми 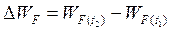 .
.
Решение:
Уровень Ферми в собственном полупроводнике определяется формулой (1.6). Из нее видно, что с увеличением температуры уровень Ферми смещается вверх от середины запрещенной зоны. Рассчитаем изменение положения уровня Ферми:
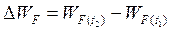
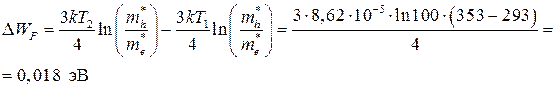
Ответ:
Уровень Ферми сместится вверх на 0,018 эВ.
ЗАДАЧА 1.8
Пластина германия n-типа имеет удельное сопротивление 0,1 Ом·см и ширину 0,25 см. К пластине приложено напряжение в 1 В. Подвижность электронов 3900 см2·В-1·с-1, дырок – 1900 см2·В-1·с-1. Концентрация собственных носителей тока 2,3×1013 см-3. Найдите плотность тока, отношение проводимостей дырками и электронами, время, которое потребуется, чтобы носители заряда пересекли пластину.
Дано:
Полупроводник (Ge) примесный n-типа.
r = 0,1 Ом×см
l = 0,25 см
U = 1 В
Подвижности μе = 3900 см2·В-1·с-1;
μh = 1900 см2·В-1·с-1;
ni = 2,3 ×1013 см-3
Найти:
Плотность тока I*;
Время, за которое носители заряда пересекут пластину τ;
Отношение проводимостей 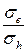 .
.
Решение:
1) Найдем плотность тока.
По определению плотность тока равна отношению тока к площади, через которую он протекает:
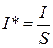 , (1.21)
, (1.21)
а силу тока можно рассчитать из закона Ома для участка цепи:
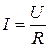 . (1.22)
. (1.22)
Зная удельное сопротивление, можно рассчитать сопротивление участка цепи:
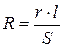 . (1.23)
. (1.23)
Подставив (1.22) и (1.23) в (1.21) получим значение плотности тока:
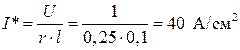
2) Найдем время пересечения носителями заряда пластины.
Время равно отношению расстояния к скорости:
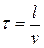 (1.24)
(1.24)
К германиевой пластине приложена разность потенциалов, т.е. движение носителей тока в ней обусловлено дрейфом. Скорость дрейфа можно найти, зная подвижность носителей тока µ и напряженность поля в пластине Е:
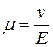 , (1.25)
, (1.25)
а напряженность поля – зная разность потенциалов U и расстояние между ними:
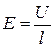 . (1.26)
. (1.26)
Подставляя (1.25) и (1.26) в (1.24), получаем:
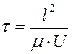 (1.27)
(1.27)
Таким образом, для электронов время прохождения пластины будет:
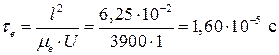 ,
,
а для дырок:
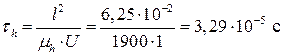 .
.
3) Найдем отношение проводимостей.
Проводимость равна обратному удельному сопротивлению:
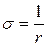 (1.28)
(1.28)
Проводимость германия n-типа при температурах, близких к комнатной, определяется в основном током электронов, т.е. из (1.12) получаем:
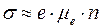 .
.
Подставляя туда (1.28) получаем значение концентрации электронов:
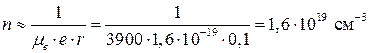 .
.
Концентрацию дырок найдем из квадрата концентрации собственных носителей тока, так же, как в задаче 1.2:
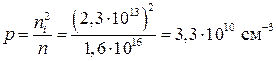 .
.
Дырочная проводимость равна:
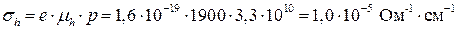
Отношение проводимостей:
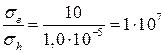 .
.
Ответ:
Плотность тока 40 А/см2.
Время пересечения пластины электронами 1,60·10-5 с, дырками – 3,29·10-5 с.
Отношение проводимости электронами к проводимости дырками –·107.
Примеры задач
1.5.1.В собственном полупроводнике ширина запрещенной зоны зависит от температуры по следующему закону Wg= 0,82 – 2·10-4·Т (эВ). Эффективные массы электрона 0,5 m, дырки 0,4 m. Для 300 К, 350 К и 400 К найдите величины концентраций собственных носителей тока и постройте график: ni= f(1/T).
1.5.2.В собственном полупроводнике при 300 К концентрация электронов в зоне проводимости 2·1013см-3. Эффективные массы электрона 0,6 m, дырки 0,45 m. Найдите ширину запрещенной зоны.
1.5.3.В собственном полупроводнике ширина запрещенной зоны 0,7 эВ. При 300 К концентрация электронов в зоне проводимости 2·1013см-3· Эффективная масса электрона в 1,5 раза больше массы дырки. Подвижность электронов при этой температуре равна 2800 см2·В-1·с-1, подвижность дырок меньше подвижности электронов в 2 раза. Найдите эффективные массы электронов и дырок и проводимость полупроводника.
1.5.4.В примесном полупроводнике n-типа ширина запрещенной зоны 0,82 эВ. Энергетический зазор между дном зоны проводимости и уровнями доноров составляет 0,02 эВ, концентрация доноров Nd = 2·1014см-3. Эффективные массы электрона 0,5 m, дырки 0,4 m. Найдите величины концентраций носителей тока при 200, 300 и 400 К.
1.5.5.В примесный полупроводник с запрещенной зоной 0,9 эВ введена донорная примесьс энергетическим зазором между дном зоны проводимости и уровнями доноров 0,022 эВ в концентрации 3·1014см-3. Эффективные массы электрона 0,6 m, дырки 0,45 m. Подвижности считать неизменными. Во сколько раз возрастет проводимость при нагревании такого полупроводника с 200 до 300 К.
1.5.6.В примесном полупроводнике p-типа ширина запрещенной зоны 0,8 эВ. Концентрация акцепторной примеси 1013см-3. Энергия акцепторных уровней 0,025 эВ. Эффективные массы электрона – 0,5 m; дырки – 0,4 m. Подвижность электронов me= 3500 см2·В-1·с-1 и me/ mh= 3 считать неизменным при выбранных температурах. Найти величины электропроводности при 250, 300 и 350 K.
1.5.7.В кремний введена примесь бора в концентрации 4·10-7 ат. %. Найдите проводимость полупроводника при комнатной температуре.
1.5.8.Через пластину германия p-типа толщиной 1 мм и площадью сечения3 мм2 при 50 оС протекает ток силой 0,02 А, разность потенциалов на границах пластины 2 В.Найдите концентрацию примеси.
1.5.9.Пластина кремния толщиной 1,5 мми площадью сечения2 мм2 легирована сурьмойв концентрации 5·1014см-3. Найдите сопротивление пластины при комнатной температуре.
1.5.10. Во сколько раз возрастет проводимость германия при 300 К, если его легировать акцепторной примесью с энергетическим зазором между потолком валентной зоны и уровнями акцепторов 0,015 эВ в концентрации 6·1015см-3?
1.5.11. При какой температуре концентрация свободных электронов в чистом кремнии будет в 3 раза больше, чем при комнатной?
1.5.12.Пластина кремния легирована донорной примесью в концентрации 2·1014см-3 и акцепторной в концентрации 1013 см-3 найдите проводимость пластины при 300 К.
Дата добавления: 2016-02-16; просмотров: 12197;
