Определение контактной разности потенциалов и ширины обедненного слоя p-n перехода в равновесном состоянии

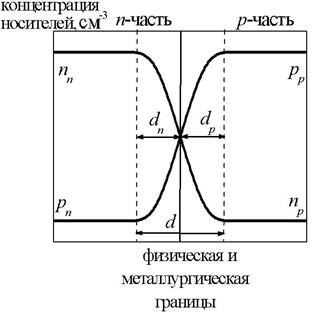
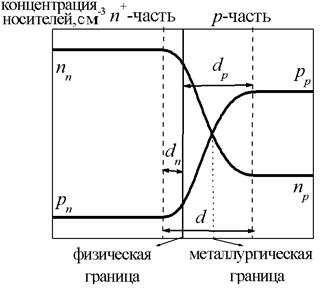
Параметры p-n перехода зависят от уровней легирования p- и n-областей, их размеров, а также от характера распределения примесей в области контакта. По соотношению уровней легирования p-n переходы подразделяют на симметричные (уровни легирования обеих частей одинаковые N_d=N_a) и несимметричные (уровни легирования разные N_d≠N_a) (рис. 2.2), а по характеру распределения примеси – на резкие и плавные.

Рис. 2.2. Симметричный и несимметричный p-n переходы

При учете зависимостей концентраций носителей заряда и уровней Ферми формулу (2.1) можно записать как:

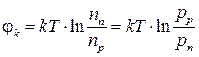* (2.2)

_______________________________

* В некоторых книгах формулы для расчета контактной разницы потенциалов записывают так: 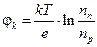. Величину 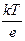[эВ] называют термическим (тепловым) потенциалом электрона, при этом используется постоянная Больцмана k равная 1,38×10^-23 Дж/К, в настоящем пособии используется k = 8,62×10⁻⁵ эВ/К, т.е. уже разделенная на заряд электрона.

Как мы видели в задаче 1.2, в области насыщения (истощения примеси) концентрации основных носителей заряда (а значит, и проводимость) не зависят от температуры и равняются концентрации примеси.

Работа в этой области обеспечивает высокую термическую стабильность параметров полупроводникового прибора, поэтому, за исключением специальных случаев, концентрации примесей подбирают так, чтобы прибор работал именно в области насыщения. В этом случае контактную разность потенциалов можно найти по формуле:

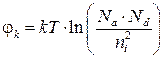(2.3)

С ростом температуры резко возрастает концентрация собственных носителей заряда n_i, это приводит к тому, что контактная разность потенциалов снижается, причем тем быстрее, чем менее легированы p- и n-области (чем меньше произведение N_a·N_d). При переходе к собственной проводимости (для большинства германиевых приборов при 100 ^оС, кремниевых – при 150 ^оС) потенциальный барьер исчезает, пространственный заряд не образуется и происходит исчезновение p-n перехода, а кристалл становится обычным омическим сопротивлением.

Ширину обедненного слоя резкого p-n перехода можно рассчитать по формуле:

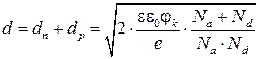(2.4)

В пределах этого слоя можно выделить две характерные границы: физическую границу между областями, легированными донорами и акцепторами и металлургическую границу, в которой наблюдается равенство концентраций основных носителей (n_n=p_p). В симметричном p-n переходе эти границы совпадают, а в несимметричном металлургическая граница сдвинута в менее легированную область. Таким образом, область пространственного заряда расширяется также в область с меньшей концентрацией примеси:

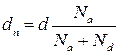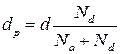и (2.5)

Напряженность электрического поля в p-n переходе максимальна на металлургической границе и равна:

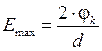(2.6)

ЗАДАЧА 2.1

Кремниевый p-n переход при 300 К. Концентрация примеси в р-области 10²² м^-3, в n-области 10²⁰ м^-3. Найдите высоту потенциального барьера (контактную разность потенциалов) и ширину обедненного слоя p-n перехода.

Дано:

p-n переход на Si.

Т = 300 К

N_а = 10²² м^-3,

N_d = 10²⁰ м^-3,

Найти:

φ_k, d

Решение:

Определим, в какую область попадает 300 К. Для этого рассчитаем концентрацию собственных носителей заряда. Согласно данным табл. 1.3:

n_i = 1,4·10¹⁰ см^-3.

Т.е. в n-области N_d = 10²⁰ м^-3 = 10¹⁴ cм^-3 >> n_i, в p-области N_а = 10²² м^-3 =
=10¹⁶ cм^-3 >> n_i. Таким образом, можно считать, что .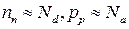

Из (2.3) контактная разность потенциалов равна:

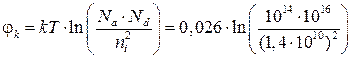=0,58 В.

Найдем ширину обедненного слоя из (2.4), причем значения концентраций будем подставлять в единых с другими величинами единицах, т.е. в м^-3:

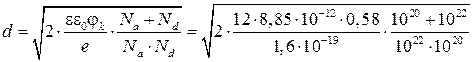= 2,8·10^-6 м.

Ответ:

Контактная разность потенциалов 0,58 В;

Ширина обедненного слоя 2,8 мкм.

ЗАДАЧА 2.2

Как изменится величина контактной разницы потенциалов кремниевого
p-n перехода при изменении температуры с 300 до 400 К? Концентрация донорной примеси 10¹³см^-3, акцепторной – 10¹⁵ см^-3.

Дано:

p-n переход на Si.

N_а = 10¹⁵ см^-3,

N_d = 10¹³ см^-3,

Т₁ = 300 К

Т₂ = 400 К

Найти:

,

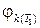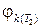
Решение:

1) При 300 K n_i(300) = 1,4·10¹⁰ см^-3, что значительно меньше N_а и N_а, поэтому можно воспользоваться формулой (2.3):

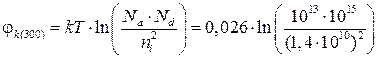=0,46 В.

2) При 400 K найдем n_i(400) по формуле (1.19):

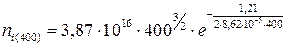=7,42·10¹² см^-3.

В этом случае p-часть диода останется в области насыщения (N_а = p_p=
= 10¹⁵ см^-3), n-часть перейдет уже в область смешанной проводимости. В этом случае для расчета контактной разницы потенциалов используем формулу(2.2):

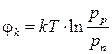
Для такого расчета нужно найти концентрацию дырок в n-части диода. По формуле (1.17) найдем концентрацию основных носителей, электронов:

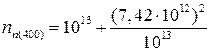=1,55·10¹³ см^-3.

Тогда концентрация дырок:

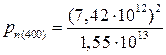=3,55·10¹² см^-3.

Контактная разница потенциалов равна:

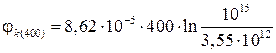=0,19 В.

Ответ:

Контактная разница потенциалов уменьшится с 0,46 до 0,19 В.