Вектор индукции магнитного поля 2 страница

Проекция dl_B на векторB_Mиндукции магнитного поля вектораdl, направленного

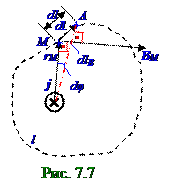
(рис. 7. 7) от данной M точки в А точку на l контуре с элементарнымdl расстоянием между ними, имеет следующий вид: dl_B= r_M dφ.(7.22)

Циркуляция вектора B индукции магнитного поля в вакууме по l контуру, т.е. при перемещении M точки, в которой определяется вектор B магнитной индукции, по этому l контуру, с учётом (7.21), (7.22) имеет следующий вид: 2π 2π ∫ Bdl = ∫ Bdl_B= (μ₀I/2π) ∫ dl_B/r = (μ₀I/2π)∫rdφ/r = (μ₀I/2π)∫dφ = μ₀I, (7.23) l l l 0 0 где I - ток силой, охватываемый l контуром; r - модуль r вектора, направленного от проводника в очередную M точку, находящуюся на l контуре, при циркуляции вектора B магнитной индукции по этому l контуру. Если l контуртока не охватывает, то циркуляция вектора B магнитной индукции по l контуру равна нулю.

Если l контурохватываетn проводников с токами I₁, I₂ … I_nсилой, каждый из которых создаёт в произвольной M точке, находящейся на l контуре, соответствующийвектор B₁_M, B₂_M, ….., B_nM индукции магнитного поля,то согласно принципу суперпозиции результирующий вектор B₀_M индукции магнитного поля в этой M точке имеет следующий вид: n B₀_M = ∑B_iM. (7.24) i = 1 Циркуляция результирующего вектора B₀ индукции магнитного поля по l контуру, который охватывает n проводников с токами I₁, I₂, …..,I_nсилой, с учётом (7.24) имеет следующий вид: n n

∫ B₀dl = ∫ ∑B_i dl = ∑ ∫B_idl.(7.25) l l i = 1 i = 1 l Каждый из интегралов ∫B_idl в (7.25) пропорционаленс учётом(7.23) току I_i силой в проводнике, где i = 1,2,…n является номером проводника, который охватывается l контуром, поэтому имеет место следующее выражение: ∫B_idl= μ₀I_i, (7.26) l где I_i - величина положительная, если ток I_iсилойна рис.7. 7 направлен на"наблюдателя", тогда вектор B индукции магнитного поля по l контуру направлен против "часовой стрелки"; I_i - величина отрицательная, если ток I_i на рис.7.7 направлен от"наблюдателя", тогда вектор B индукции магнитного поля по l контуру направлен по"часовой стрелке". Подставляем (7.26) в (7.25) и получаем следующее выражение циркуляции результирующего вектора B₀ индукции магнитного поля в вакууме по l контуру, т.е. при перемещении M точки по этому l контуру, который охватывает n проводников с токами I₁, I₂, …..,I_nсилой: ∫ B₀ dl= μ₀∑I_i. (7.27) l i = 1 Теорема о циркуляции вектора индукции магнитного поля в интегральной виде имеет своё математическоевыражение (7.27): циркуляция результирующего вектора B₀ индукции магнитного поля по l контуру в вакууме, который охватывает n проводников с токами I₁, I₂ … I_nсилой, равняется алгебраическойсумме этих токов, умноженной на μ₀ -магнитнуюпостоянную. Если токи текут через поверхность S площадью, охватываемую l контуром, с вектором

j плотноститока через элементарную поверхность dS площадью, а n - положительнаянормаль к этой поверхности dS площадью, то суммирование(7.27) токов в каждом из n проводников заменяем интегрированиемпо поверхности S площадью, вследствие чего для результирующего тока I₀силой через поверхность S площадью,охватываемую этим l контуром, имеет место следующее выражение: n

I₀ = ∑I_i = ∫j dS = ∫jndS. (7.28)

i = 1 S S

Подставляем (7.28) в (7.27) и получаем следующее математическое выражение теоремы в интегральном виде о циркуляции результирующего вектора B₀ магнитной индукции, согласно которомуциркуляция результирующего вектора B₀ магнитной индукции по l контуру в вакууме равна интегралу от токов с вектором j плотности, пересекающих поверхность S площадью, которую охватывает этот l контур: ∫ B₀ dl=μ₀∫j dS. (7.29) l S Заменим в (7.29) по теореме Стокса (5.41) из раздела 5.1 «Электрическое поле системы неподвижных зарядов в вакууме. Теорема Гаусса для электростатического поля. Работа и потенциал электростатического поля» интегралпо контуру поверхностныминтегралом по поверхности S площадью, которую охватывает этот l контур и получим следующую теорему о циркуляции результирующего вектора B₀ индукции магнитного поля в вакууме в дифференциальномвиде: ∫ B₀ dl= ∫ [B₀ ] dS = μ₀ ∫j dS ↔[ B₀ ] = μ₀j. (7.30) l S S Согласно (7.30) ротор [ B₀ ] = rot B₀(5.42) из раздела 5.1 «Электрическое поле системы неподвижных зарядов в вакууме. Теорема Гаусса для электростатического поля. Работа и потенциал электростатического поля» результирующего вектора B₀ индукции магнитного поля в вакууме в произвольной точке пространства пропорционален вектору j плотноститока в этой точке пространства.

Расчет магнитного поля соленоида с постоянным током в вакууме

Соленоид- это длинная (рис.7. 8) тонкостенная диэлектрическая трубка, на которую намотан проводник с током Iсилойи количеством n витковна единицу длины. Линейнаяj_линплотностьтока всоленоидеимеет следующий вид: j_лин = nI. (7.31) В сечении A - A магнитные потоки (7.18) Ф_m = BS через внутреннее и Ф_m' = B' S' внешнее сечения соленоидасоответственно S, S' площадьювследствие замкнутости линий магнитногополя одинаковы, поэтому имеет место следующее равенство: BS = B'S', (7.32)

где B и B' - соответственно модули векторовB и B' индукции магнитного поля внутрии вне соленоида. Т.к. S' площадь вне соленоида бесконечна, а магнитный поток через внешнее Ф_m' = B' S' сечение соленоида величина конечная, то имеет место следующее равенство: B' = 0. (7.33) Циркуляция (7.23) векторов B и B' индукции магнитного поляв вакууме внутрии вне соленоидапо контуру 1 - 2 - 3 - 4 с учётом (7.33), т.е. наличия только вектораB индукции магнитного

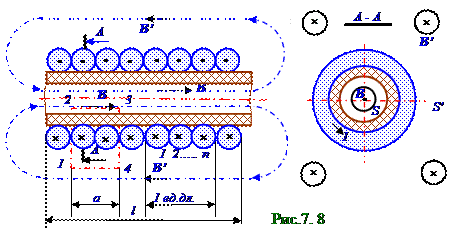
поляв вакууме внутри соленоида, направленного вдоль 2 -3 отрезкаa длиной, а также с учётом (7.31) охвата1 - 2 -3 -4 контуром na проводников, по которым протекает ток I силой, имеет следующий вид: ∫ Bdl =∫ Bdl_B =Ba = μ₀ naI ↔ 1 - 2 -3 -4 2 -3 ↔ B = μ₀nI.(7.34)Выражение (7.34) справедливо в середине(рис.07. 0.8) длины соленоида. У конца соленоида

модуль B вектораB индукциимагнитного поля в вакууме имеет следующий вид: B = μ₀nI/2.(7.35)

Расчет магнитного поля тороида с постоянным током в вакууме

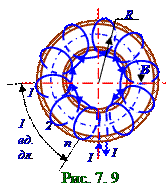
В тороиде(рис. 7. 9) проводник с током I силойнамотан на тонкостенный диэлектрический тор n количеством витковна единицу длины. Внутри тороида вектор B индукции в вакууме направлен вдоль линиймагнитного поля, имеющих форму окружностей с R радиусом.Вне тороида вектор B' индукции магнитного поля по аналогии (7.33) равен нулю.Циркуляция (7.27) вектора B индукции магнитного поляв вакууме внутри тороидапоокружности с R радиусом с учётом (7.23),

т.е. наличия только вектора B, касательного в каждой точке окружности2πR длиной, а также с учётом (7.31) охватаэтой окружностью2πRn проводников, по которым протекает ток Iсилой, имеет следующий вид: ∫ Bdl = ∫ Bdl_B = B2πR= μ₀2πRnI ↔ B = μ₀nI. (7.36) 2πR 2πR Математические (7.34) и (7.36) выражения модулей B векторов B индукциимагнитного поля в вакууме внутрисоответственно длинного соленоидаи тороида совпадают.

Лекция 6. Движение заряженных частиц в электрическом и магнитном полях

Сила Лоренца. Движение заряженной нерелятивистскойчастицы в однородном магнитном поле. Движение заряженной релятивистской частицы в однородном магнитном поле. Отклонение движущихся заряженных частиц электрическими и магнитными полями. Эффект Холла. Определение удельного заряда нерелятивистскогои релятивистского электрона. Определение удельного заряда ионов. Масс - спектрографы. Ускорители заряженных частиц. Циклотрон. Синхрофазотрон.

Сила Лоренца

Вектор F_e силы, который действует при отсутствии магнитногополя со стороны электрическогополя на нерелятивистскуюили релятивистскую частицу с q₊положительным или

q_- отрицательным зарядом согласно (5.3) из раздела 5.1 «Электрическое поле системы неподвижных зарядов в вакууме. ТеоремаГауссадля электростатического поля. Работа и потенциал электростатического поля» имеет следующий вид: F_e= qE, (7.37) где при q₊положительном заряде вектор F_e силы коллинеаренвектору E напряженности электрического поля и направлен с ним в одну сторону, а в случае сq_- отрицательным зарядом вектор F_э силы коллинеаренвектору E напряженности электрического поля и направлен с ним в противоположную сторону.

МодульE и направление (5.3) из раздела 5.1 «Электрическое поле системы неподвижных зарядов в вакууме. Теорема Гаусса для электростатического поля. Работа и потенциал электростатического поля» вектора E напряженности электрического поля при отсутствии магнитногополя определяет (7.37) модульF_e и направление вектора F_e силы, который действует на нерелятивистскуюили релятивистскую частицу с

q₊положительным или q_- отрицательным зарядом. Поэтому вектор E напряженности электрического поля при отсутствии магнитногополя является силовой характеристикой длянерелятивистскойили релятивистской частицы с q₊положительным или q_- отрицательным зарядом.

Вектор F_m силы, который действует со стороны магнитногополя на нерелятивистскуюили релятивистскую частицу с q₊положительным или q_- отрицательным зарядом согласно имеет следующий вид: F_m= q[v, B], (7.38)

где при q₊положительном заряде вектор F_m силы коллинеарен векторному [v, B] произведениюинаправлен с ним в одну сторону от (рис.7.2) векторов v скоростииB индукции магнитного поля в точке нахождения в данный момент t времени электрически заряженной частицы; при q_- отрицательном заряде вектор F_m силы коллинеарен векторному [v, B] произведениюинаправлен с ним в противоположную сторону от (рис.7.2) векторов v скоростииB индукции магнитного поля в точке нахождения в данный момент t времени электрически заряженной частицы.

Вектор F силы Лоренца, который действует на нерелятивистскуюили релятивистскую частицу с q₊положительным или q_- отрицательным зарядом при её движении в пространстве, где одновременносуществует электрическоеи магнитноеполе, имеет согласно (8.82), (8.83) следующий вид: F = F_e + F_m = qE+ q[v, B]. (7.39)

Выражение (7.39) справедливо для постоянных из параграфа "Электрический заряд. Закон Кулона" из раздела 5.1 «Электрическое поле системы неподвижных зарядов в вакууме. Теорема Гаусса для электростатического поля. Работа и потенциал электростатического поля» и переменныхво t времени электрических полей, а также справедливо для постоянных(7.6) " и переменныхво t времени магнитных полей.

Вектор F силы Лоренца, который действует на частицу с q₊положительным или q_- отрицательным зарядом при её отсутствии движения в пространстве, где существует только магнитноеполе, т.е. (7.37) вектор E напряженности электрического поля равен нулю,тоже (7.38) равен нулю. В этом существенное отличие магнитного поля от электрического, а именно: магнитноеполедействуеттолько на движущийся заряд.

МодульB и направление (7.6) вектора B индукции магнитного поля при отсутствии электрического поля определяет (7.38) модульF_m и направление вектора F_m силы, который действует на движущуюся с вектором v скоростинерелятивистскуюили релятивистскую частицу с q₊положительным или q_- отрицательным зарядом. Поэтому вектор B индукции магнитного поля при отсутствии электрического поля является силовой характеристикой движущейся с вектором v скоростинерелятивистскойили релятивистской частицы с с q₊положительным или q_- отрицательным зарядом.

Согласно (7.38) вектор F_m силы, который действует на движущуюся с вектором v скоростинерелятивистскуюили релятивистскую частицу сq₊положительным или q_- отрицательным зарядом всегда перпендикулярен этому вектору v скорости, поэтому (1.82) из раздела 1.0 "Физические основы механики" работаA этоговектора F_m силы со стороны постоянного магнитногополя по перемещениюэлектрически заряженной частицыравна нулю.

Движение заряженной нерелятивистскойчастицы в однородном магнитном поле

На (рис. 7.10) нерелятивистскаячастица, например, имеющая q₊положительный заряд и движущаяся при отсутствии электрического поля с вектором v скоростив вакууме во внешнем однородном магнитном полес вектором B индукции этого магнитного поля, действует(7.38) следующий векторF_m силы Лоренца: F_m= q₊[v, B] ↔ F_m = q₊vBsinα = q₊v_┴B, (7.40)

где F_m -модуль вектора F_m силы Лоренца, направленного к центру окружности R радиусом, по которой

с v_┴модулем вектораv_┴перпендикулярной составляющей вектора v скорости двигается q₊положительный заряд; α -угол, под которым q₊положительный заряд с вектором v скорости первоначально двигался в вакуумевOYZ плоскости неподвижной OXYZ системы координат до момента t₀ времени попадания в область однородногомагнитного поля с вектором B индукции этого магнитного поля.

Кроме (рис. 7.10) движения q₊положительного заряда по окружности R радиусом он двигается прямолинейно по OY оси неподвижной OXYZ системы координат с вектором

v_\\ составляющей вектора v скорости,параллельнымвектору B индукции внешнего однородного магнитного поля,поэтому траекториейдвижения этого q₊положительного заряда во внешнем однородном магнитном полебудет спираль.

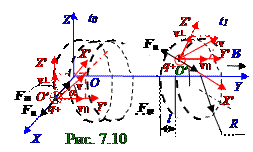
ПодвижнаяO′X′Y′Z′ система координат связана с q₊положительным зарядом, вследствие чего она вместе с этим q₊положительным зарядом двигается равномерно по OY оси неподвижной OXYZ системы координат с векторомv_\\ составляющей вектора v скорости,параллельным вектору B индукции внешнего однородного магнитного поля, а также (рис.1.1) из раздела 1.0 "Физические основы механики" равномерно двигается по окружности R радиуса с центром,

лежащим на OY оси неподвижной OXYZ системы координат, с постоянным по модулюv_┴ вектором

v_┴ скорости и вектором a_n нормальногоускорения, направленного по O′X′ оси подвижнойO′X′Y′Z′ системы координат.

Модуль a_n вектора a_n нормальногоускорения (1.16) из раздела 1.0 "Физические основы механики"для обозначений, принятых на рис. 7.10, имеет следующий вид: a_n = v_┴²/R. (7.41)Проекция на O′X′ ось (1.46) из раздела 1.0 "Физические основы механики"второго законаНьютонав неинерциальной подвижнойO′X′Y′Z′ системе координат, поскольку эта подвижнаяO′X′Y′Z′ система координат двигается (рис. 08.0.11) вместе с q₊положительным зарядом с вектором a_n нормальногоускорения по спирали, с учётом направления вектора F_и инерциальнойсилы в отрицательную сторону O′X′ оси подвижнойO′X′Y′Z′ системы координат и направления (8.86) вектораF_m силы Лоренца в положительную сторону O′X′ оси подвижнойO′X′Y′Z′ системы координат и без учёта силы тяжести этого q₊положительного заряда m массыимеет следующий вид:

O′X′: 0 = F_и_X_'+ F_mX_'= - ma_n + q₊v_┴B ↔ 0 = - m(v_┴²/R) + q₊v_┴B ↔ R = mv_┴/q₊B ↔ T = 2πR/ v_┴ ↔ T = = 2πm/q₊B, (7.42)

где F_и_X_'= - ma_n= - m(v_┴²/R) - отрицательноезначениепроекции на O′X′ ось вектора F_иинерциальнойсилы, поскольку этот вектор F_иинерциальнойсилы направлен вотрицательную сторону O′X′ оси подвижнойO′X′Y′Z′ системы координат; F_mX_'= q₊v_┴B - положительноезначениепроекции на O′X′ ось (8.84) вектора F_mсилы, поскольку этот вектор F_m силы направлен в положительную сторону O′X′ оси подвижнойO′X′Y′Z′ системы координат; q=|q_-| -модуль отрицательного заряда.; T -период полного оборота q₊положительного заряда m массыпо окружности R радиуса с центром, лежащим на OY оси неподвижной OXYZ системы координат, не зависит согласно (8.88) от модуля v_┴вектора

v_┴перпендикулярной составляющей вектора v скорости движения заряженной частицы.

Расстояние l между соседнимивитками (рис. 7.10) спиралиопределяется из следующего расчёта пути l величиной, который q₊положительный заряд m массыс модулем v_\\вектора

Дата добавления: 2016-02-14; просмотров: 1085;