Показатели вариации

Средняя величина дает обобщающую характеристику признака изучаемой совокупности, но она не показывает, как располагаются около нее варианты осредняемого признака, сосредоточены ли они вблизи средней или значительно отклоняются от нее. Это имеет значение для характеристики надежности средней.

Чем больше варианты отдельных единиц совокупности различаются между собой, тем больше они отличаются от своей средней, и наоборот. Следовательно, нужны показатели, характеризующие отклонения отдельных значений от общей средней.

Вариация – изменение величины признака при переходе от одной единицы совокупности к другой.

Для измерения вариации в статистике используют следующие показатели: размах вариации, среднее линейное отклонение, дисперсия и среднее квадратическое отклонение, коэффициент вариации.

Ø Размах вариации (R) представляет собой разность между максимальным и минимальным значениями признака:

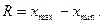
Ø Среднее линейное отклонение 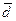представляет собой среднюю арифметическую абсолютных значений отклонений отдельных вариантов от их средней арифметической (при этом всегда предполагают, что среднюю вычитают из варианта: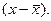

Среднее линейное отклонение:

для несгруппированных данных 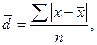где п – число членов ряда;

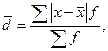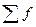для сгруппированных данных где - сумма частот вариационного ряда.

Среднее линейное отклонение как меру вариации применяют редко (только в тех случаях, когда суммирование показателей без учета знаков имеет экономический смысл). С его помощью, например, анализируется состав работающих, ритмичность производства, оборот внешней торговли.

Ø Дисперсия признака представляет собой средний квадрат отклонений вариантов от их средней величины, она вычисляется по формулам простой и взвешенной дисперсии (в зависимости от исходных данных):