Правило сложения дисперсий

Правило сложения дисперсий гласит, что общая дисперсия ( 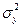) может быть разложена на две составные части: 1) межгрупповую ( 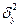) и 2) среднюю из внутригрупповых ( )

.

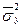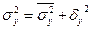Общая дисперсия 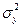измеряет вариацию результативного признака по всей совокупности под влиянием всех факторов, обусловивших эту вариацию. Она равна среднему квадрату отклонений отдельных значений результативного признака от его средней величины и может быть вычислена как простая дисперсия или взвешенная.

.

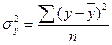Межгрупповая дисперсия 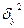характеризует систематическую вариацию результативного признака, обусловленную влиянием признака-фактора, положенного в основание группировки. Она равна среднему квадрату отклонений групповых (частных) средних 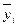от общей средней :

,

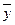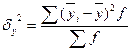где 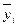- среднее значение признака i-й группы; f – численность единиц в группе.

Внутригрупповая дисперсия 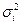отражает случайную вариацию, т.е. часть вариации, обусловленную влиянием неучтенных факторов и не зависящую от признака-фактора, положенного в основание группировки. Она равна среднему квадрату отклонений отдельных значений результативного признака внутри группы у от средней арифметической этой группы 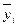(групповой средней) и может быть исчислена как простая дисперсия или как взвешенная дисперсия по формулам, соответственно:

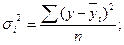
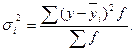
На основании внутригрупповой дисперсии по каждой группе можно определить общую среднюю из внутригрупповых дисперсий:

.

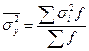Пользуясь правилом сложения дисперсий, можно всегда по двум известным дисперсиям определить третью – неизвестную, а также судить о силе влияния группировочного признака.

В статистическом анализе широко используется эмпирический коэффициент детерминации ( 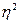) – показатель, представляющий собой долю межгрупповой дисперсии в общей дисперсии результативного признака и характеризующий силу влияния группировочного признака на образование общей вариации:

.

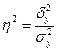Эмпирический коэффициент детерминации показывает долю вариации результативного признака у под влиянием факторного признака х. При отсутствии связи коэффициент детерминации равен нулю, а при функциональной связи – единице.

Эмпирическое корреляционное отношение – это корень квадратный из эмпирического коэффициента детерминации:

,

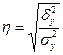оно показывает тесноту связи между группировочным и результативным признаками.

Эмпирическое корреляционное отношение, как и коэффициент детерминации, может принимать значения от 0 до 1.

Чем значение корреляционного отношения ближе к единице, тем теснее, ближе к функциональной зависимости связь между признаками.

Для качественной оценки тесноты связи на основе показателей эмпирического корреляционного отношения можно воспользоваться шкалой Чэддока:

Пример. (Гусаров)

Пусть при изучении влияния квалификации (тарифного разряда) рабочих на уровень производительности труда в цехе были получены данные, представленные в табл.

Таблица

Распределение рабочих по среднечасовой выработке изделий

№ п/п	Рабочие IV разряда	№ п/п	Рабочие V разряда
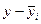
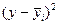
Выработка рабочего, шт. (yi)			Выработка рабочего, шт. (yi)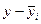
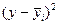
		-3				-1
		-1				-1
		-1
Σ		-		Σ		-

Для результативного признака исчислить:

1) групповые дисперсии;

2) среднюю из внутригрупповых дисперсий;

3) межгрупповую дисперсию;

4) общую дисперсию;

5) проверить правильность сложения дисперсий.

В этом примере данные группируются по квалификации (тарифному разряду) рабочих, являющейся факторным признаком х.

Результативный признак y варьирует как под влиянием систематического фактора х – квалификации (межгрупповая вариация), так и других неучтенных случайных факторов (внутригрупповая вариация). Задача заключается в измерении этих вариаций с помощью дисперсий: общей, межгрупповой и внутригрупповых.

1. Для расчета групповых дисперсий исчислим средние выработки по каждой группе и общую среднюю выработку, шт.:

по первой группе ;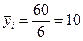

по второй группе ;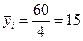

по двум группам .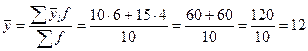

Данные для расчета дисперсий по группам представлены в табл. Подставив необходимые значения в формулу, получим внутригрупповые дисперсии:

по первой группе ;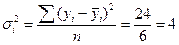

по второй группе .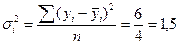

Внутригрупповые дисперсии показывают вариации выработки в каждой группе, вызванные всеми возможными факторами (техническое состояние оборудование, обеспеченность инструментами и материалами, возраст рабочих, интенсивность труда и т.д.), кроме различий в квалификационном разряде (внутри группы все рабочие имеют одну квалификацию).

2.Рассчитаем среднюю из внутригрупповых дисперсий по формуле:

.

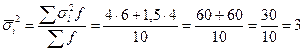Средняя из внутригрупповых дисперсий отражает вариацию выработки, обусловленную всеми факторами, кроме квалификации рабочих, но в среднем по всей совокупности.

3.Исчислим межгрупповую дисперсию по формуле:

.

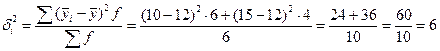Межгрупповая дисперсия характеризует вариацию групповых средних, обусловленную различиями групп рабочих по квалификационному разряду.

4. Исчислим общую дисперсию по формуле:

.

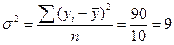Общая дисперсия отражает суммарное влияние всех возможных факторов на общую вариацию среднечасовой выработки изделий всеми рабочими цехами.

5.Суммирование средней из внутригрупповых дисперсий и межгрупповой дает общую дисперсию:

.

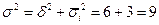Очевидно, чем больше доля межгрупповой дисперсии в общей дисперсии, тем сильнее влияние группировочного признака (классификационного разряда) на изучаемый признак (количество изготовляемых изделий).