Показатели анализа динамических рядов
Анализ скорости и интенсивности развития явления во времени осуществляется с помощью аналитических показателей, которые получаются в результате сравнения уровней ряда динамики между собой. К таким показателям относятся:
- абсолютный прирост;
- темпы роста;
- темпы прироста;
- темпы наращивания;
- абсолютное значение одного процента прироста.
При этом принято сравниваемый уровень называть отчетным, а уровень, с которым производят сравнение, - базисным.
Система средних показателей динамики включает:
- средний уровень ряда;
- средний абсолютный прирост;
- средний темп роста;
- средний темп прироста.
Общеупотребительные обозначения уровней рядов динамики следующие:
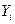- данный уровень;
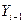- предыдущий уровень;
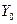- базисный уровень;
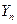- конечный уровень;
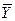- средний уровень.
Первый аналитический показатель – абсолютный прирост (снижение) уровней исчисляется разницей между двумя уровнями:
цепной абсолютный прирост
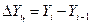
базисный абсолютный прирост
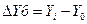
Цепные и базисные абсолютные приросты взаимосвязаны:
· сумма цепных абсолютных приростов равна конечному базисному абсолютному приросту;
· разность между двумя смежными базисными приростами равна промежуточному цепному.
Обобщением цепных абсолютных приростов за период является средний абсолютный прирост:
,
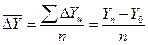где п – число цепных абсолютных приростов;
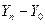- конечный базисный абсолютный прирост.
Показатель интенсивности изменения уровня ряда в зависимости от того, выражается ли он в виде коэффициента или в процентах, принято называть коэффициентом роста (k)или темпом роста (T):
Темп роста цепной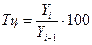 
;
темп роста базисный: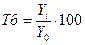 
.
Коэффициент ростапоказывает, во сколько раз данный уровень больше базисного уровня (если этот коэффициент больше единицы) или какую часть базисного уровня составляет уровень текущего периода за некоторый промежуток времени (если он меньше единицы).В качестве базисного уровня может приниматься какой-то постоянный для всех уровень (часто начальный уровень ряда) либо для каждого последующего предшествующий ему. В первом случае говорят о базисных коэффициентах роста, во втором – о цепных коэффициентах роста.
Между цепными и базисными коэффициентами роста существует взаимосвязь:
- произведение последовательных цепных коэффициентов роста равно базисному коэффициенту роста за весь период;
- частное от деления двух смежных базисных коэффициентов роста равно промежуточному цепному.
Обобщением цепных темпов роста за период является средний темп роста, который исчисляют по формулам:
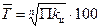, или 
,
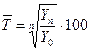где Π – произведение цепных коэффициентов роста.
Темп прироста показывает, на какую долю (или процент) уровень данного периода или момента времени больше (или меньше) базисного уровня. Чаще всего определяется как разность между темпами роста и 100%.
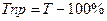
или по формулам:
цепной темп прироста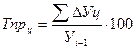 
;
базисный темп прироста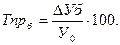 
Если темп роста всегда положительное число, то темп прироста может быть положительным, отрицательным и равным нулю.
Средний темп прироста может быть найден вычитанием 100% из среднего темпа роста:
.
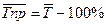Абсолютное значение одного процента прироста представляет собой одну сотую часть базисного уровня и в то же время – отношение абсолютного прироста к соответствующему темпу прироста. Оно показывает, какое абсолютное значение скрывается за относительным показателем – одним процентом прироста.
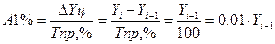
Перечисленные выше показатели обычно представляют в таблице.
Средний уровень интервального ряда динамики в случае равенства этих интервалов определяется по формуле:
.
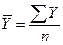Средний уровень для моментного ряда в случае, если временные расстояния между этими моментами (датами) одинаковы, определяется по формуле средней хронологической
,
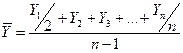где п – число уровней ряда.
Пример. Расчет показателей динамики.
Динамика выручки предприятия
| Годы | Выру-чка млн. руб. | Абсолютный прирост, млн. руб. | Темп роста, % | Темп прироста, % | Абсо-лютное значение 1% прироста, тыс. руб. | ||||
| цепной | базис–ный | цепной | базис–ный | цепной | базис–ный | ||||
| 26,3 | - | - | - | - | - | - | |||
| 28,5 | +2,2 | +2,2 | 108,4 | 108,4 | +8,4 | +8,4 | |||
| 24,2 | -4,3 | -2,1 | 84,9 | 92,0 | -15,1 | -8,0 | |||
| 25,4 | +1,2 | -0,9 | 105,0 | 96,6 | +5,0 | -3,4 | |||
| 27,0 | +1,6 | +0,7 | 106,3 | 102,7 | +6,3 | +2,7 | |||
| 30,6 | +3,6 | +4,3 | 113,3 | 116,3 | +13,3 | +16,3 |
· Абсолютный прирост
цепной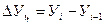 
базисный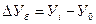 
2008 г. 28,5 – 26,3 = +2,2 млн. руб. 28,5 – 26,3 = +2,2 млн. руб.
2009 г. 24,2 – 28,5 = - 4,3 млн. руб. 24,2 – 26,3 = - 2,1 млн. руб.
2010 г. 25,4 – 24,2 = +1,2 млн. руб. 25,4 – 26,3 = - 0,9 млн. руб.
2011 г. 27,0 – 25,4 = +1,6 млн. руб. 27,0 – 26,3 = +0,7 млн. руб.
2012 г. 30,6 – 27,0 = + 3,6 млн. руб. 30,6 – 26,3 = +4,3 млн. руб.
· Темп роста
цепной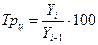 
базисный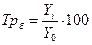 
2008 г. (28,5 : 26,3)*100 = 108,4% (28,5 : 26,3)*100 = 108,4%
2009 г. (24,2 : 28,5)*100 = 84,9% (24,2 : 26,3)*100 = 92,0%
2010 г. (25,4 : 24,2)*100 = 105,0% (25,4 : 26,3)*100 = 96,6%
2011 г. (27,0 : 25,4)*100 = 106,3% (27,0 : 26,3)*100 = 102,7%
2012 г. (30,6 : 27,0)*100 = 113,3% (30,6 : 26,3)*100 = 116,3%
· Темп прироста
цепной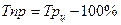 
базисный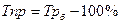 
2008 г. 108,4 – 100 = +8,4% 108,4 – 100 = +8,4%
2009 г. 84,9 – 100 = - 15,1% 92,0 – 100 = - 8,0%
2010 г. 105,0 – 100 = +5,0% 96,6 – 100 = - 3,4%
2011 г. 106,3 – 100 = +6,3% 102,7 – 100 = +2,7%
2012 г. 113,3 – 100 = +13,3% 116,3 – 100 = +16,3%
· Абсолютное значение 1% прироста
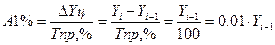
2008 г. 0,01 * 26,3 = 0,263 млн. руб. (или 263 тыс. руб.)
2009 г. 0,01 * 28,5 = 0,285 млн. руб. (или 285 тыс. руб.)
2010 г. 0,01 * 24,2 = 0,242 млн. руб. (или 242 млн. руб.)
2011 г. 0,01 * 25,4 = 0,254 млн. руб. (или 254 тыс. руб.)
2012 г. 0,01 * 27,0 = 0,270 млн. руб. (или 270 тыс. руб.)
Средние показатели
· средний уровень ряда
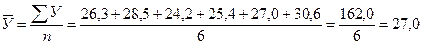млн. руб.
· средний абсолютный прирост
как средняя арифметическая простая цепных приростов:
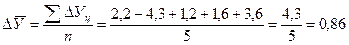млн. руб.
или как отношение базисного прироста к числу периодов без одного:
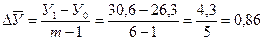млн. руб.
· Средний коэффициент роста
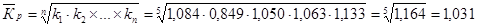
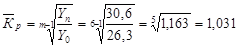
· Средний темп роста
· 
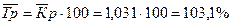
· Средний темп прироста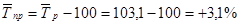 
.
Особенности применения средней хронологической
· при наличии исчерпывающих данных об изменении моментного ряда с неравными промежутками времени между датами используется формула:
,
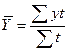где у – уровни, сохранившиеся без изменения в течение времени t.
Пример 1. На 1 января 2013 г. остаток по вкладу составлял 5500 руб. В течение I квартала имели место следующие изменения величины остатков вклада (руб.) (табл. 1).
Таблица 1
Остатки по вкладу в банке за I квартал
| 5 января | 17 января | 21 февраля | 13 марта | 20 марта | 28 марта |
| +1500 | -2000 | -3000 | +7000 | +1700 | -2300 |
Определить средний остаток по вкладу за I квартал.
Решение:
Результаты расчета сведены в табл. 2.
Таблица 2
Результаты расчета среднего размера вклада
| Период | Число дней в периоде, t | Размер вклада (руб.), y | yt |
| 01.01 – 05.01 | 22 000 | ||
| 05.01 – 17.01 | 84 000 | ||
| 17.01 – 21.02 | 175 000 | ||
| 21.02 – 13.03 | 40 000 | ||
| 13.03 – 20.03 | 63 000 | ||
| 20.03 – 28.03 | 10 700 | 85 600 | |
| 28.03 – 01.04 | 33 600 | ||
| Итого | - | 503 200 |
Средний остаток по вкладу составляет: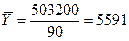 
руб.
· для моментного ряда динамики с неравными промежутками времени между датами используется формула:
,
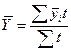где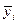 
- средние уровни в интервале между датами;
t – интервал времени.
Пример 2. Имеются следующие данные о товарных запасах розничного магазина, млн. руб.: на 1 января 2012 г. – 37; на 1 мая 2012 г. – 63; на 1 августа – 57; на 1 января 2013 г. – 71.
Исчислить среднегодовой товарный запас магазина за 2012 г.
Решение:
Средние уровни товарных запасов Число месяцев (t) между
за периоды: моментами времени:
с 01.01 по 01.05 – (37 + 63) : 2 = 50; 4
с 01.05 по 01.08 – (63 + 57) : 2 = 60; 3
с 01.08 по 01.01 – (57 + 71) : 2 = 64. 5
Средний уровень товарных запасов за год составит:
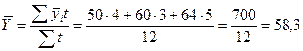млн. руб.
· для моментного ряда динамики с равными промежутками времени между датами используется формула – средняя хронологическая простая.
Пример 3. Имеются следующие данные об остатках сырья и материалов на складе предприятия, тыс. руб.: на 1 января – 500; на 1 февраля – 570; на 1 марта – 585; на 1 апреля – 490.
Определить среднемесячный остаток сырья и материалов на складе предприятия за I квартал.
Решение:
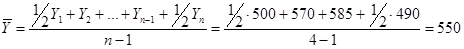
Дата добавления: 2016-02-16; просмотров: 1340;