Агрегатная форма общего индекса
Основной формой общих индексов являются агрегатные индексы.
Достижение в сложных статистических совокупностях сопоставимости разнородных единиц осуществляется введением в индексные отношения специальных сомножителей индексируемых величин. Такие сомножители называются соизмерителями. Они необходимы для перехода от натуральных измерителей разнородных единиц статистической совокупности к однородным показателям. При этом в числителе и знаменателе общего индекса изменяется лишь значение индексируемой величины, а их соизмерители являются постоянными величинами.
В качестве соизмерителей индексируемых величин выступают тесно связанные с ними экономические показатели: цены, количество и др.
Произведение каждой индексируемой величины на соизмеритель образует в индексном отношении определённые экономические категории.
При определении общего индекса цен в агрегатной форме 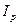 в качестве соизмерителя индексируемых величин
в качестве соизмерителя индексируемых величин 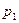 и
и 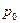 могут приниматься данные о количестве реализации товаров в текущем периоде
могут приниматься данные о количестве реализации товаров в текущем периоде 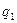 . При умножении
. При умножении 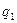 на индексируемые величины в числителе индексного отношения образуется значение
на индексируемые величины в числителе индексного отношения образуется значение 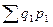 , сумма стоимости продажи товаров в текущем периоде по ценам того же текущего периода. В знаменателе индексного отношения образуется значение
, сумма стоимости продажи товаров в текущем периоде по ценам того же текущего периода. В знаменателе индексного отношения образуется значение 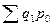 , т.е. сумма стоимости продажи товаров в текущем периоде по ценам базисного периода.
, т.е. сумма стоимости продажи товаров в текущем периоде по ценам базисного периода.
Агрегатная формула такого общего индекса цен имеет следующий вид:
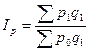
 (1)
(1)
Расчёт агрегатного индекса цен по данной формуле предложил немецкий экономист Г. Пааше, поэтому он называется индексом Пааше.
При другом способе определения агрегатного индекса цен в качестве соизмерителя индексируемых величин 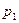 и
и 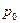 могут применяться данные о количестве реализации товаров в базисном периоде
могут применяться данные о количестве реализации товаров в базисном периоде 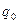 . При этом умножение
. При этом умножение 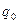 на индексируемые величины в числителе индексного отношения образует значение
на индексируемые величины в числителе индексного отношения образует значение 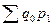 , т.е. сумму стоимости продажи товаров в базисном периоде по ценам текущего периода.
, т.е. сумму стоимости продажи товаров в базисном периоде по ценам текущего периода.
В знаменателе индексного отношения образуется значение 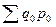 , т.е. сумма стоимости продажи товаров в базисном периоде по ценам того же базисного периода.
, т.е. сумма стоимости продажи товаров в базисном периоде по ценам того же базисного периода.
Агрегатная формула такого общего индекса имеет вид:
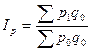 (2)
(2)
Расчёт общего индекса цен по данной формуле предложил немецкий экономист Э. Ласпейрес, и получил название индекса Ласпейреса.
Индексы Пааше и Ласпейреса характеризуют различные качественные особенности изменения цен.
Индекс Пааше характеризует влияние изменения цен на стоимость товаров, реализованных в отчётном периоде. Индекс Ласпейреса показывает влияние изменения цен на стоимость количества товаров, реализованных в базисном периоде.
Другим важным видом общих индексов, которые широко применяются в статистике, являются агрегатные индексы физического объёма товарной массы.
При определении агрегатного индекса физического объёма товарной массы 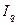 в качестве соизмерителей индексируемых величин
в качестве соизмерителей индексируемых величин 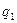 и
и 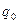 могут применяться неизменные цены базисного периода
могут применяться неизменные цены базисного периода 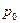 . При умножении
. При умножении 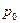 на индексируемые величины в числителе индексного отношения образуются значение
на индексируемые величины в числителе индексного отношения образуются значение 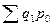 , т.е. сумма стоимости товарной массы текущего периода в базисных ценах. В знаменателе —
, т.е. сумма стоимости товарной массы текущего периода в базисных ценах. В знаменателе — 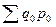 , т.е. сумма стоимости товарной массы базисного периода в ценах того же базисного периода.
, т.е. сумма стоимости товарной массы базисного периода в ценах того же базисного периода.
Агрегатная форма общего индекса имеет следующий вид:
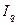 =
= 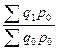 (3)
(3)
Поскольку, в числителе формулы 3 содержится сумма стоимости реализации товаров в текущем периоде по неизменным (базисным) ценам, а в знаменателе — сумма фактической стоимости товаров, реализованных в базисном периоде в тех же неизменных (базисных) ценах, то данный индекс является агрегатным индексом товарооборота в сопоставимых (базисных) ценах.
Агрегатный индекс физического объёма товарооборота может определяться посредством использования в качестве соизмерителя индексируемых величин 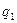 и
и 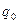 цен текущего периода
цен текущего периода 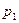 .
.
Агрегатная формула общего индекса будет иметь вид:
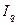 =
= 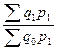 (4)
(4)
Аналогичным образом производится расчёт индекса себестоимости, при этом сравниваются суммы затрат в производстве в отчётном периоде ( 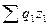 — числитель индекса) с суммой затрат в производстве на продукцию отчётного периода по себестоимости базисного периода (
— числитель индекса) с суммой затрат в производстве на продукцию отчётного периода по себестоимости базисного периода ( 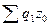 — знаменатель).
— знаменатель).
В теории индексов обычно придерживаются следующего правила:
· индексы качественных показателей строятся с весами отчетного периода (при этом в роли соизмерителей используется какой-либо количественный показатель);
· индексы количественных показателей строятся с весами базисного периода (в этом случае соизмерителем служит какой-либо качественный показатель).
Такое построение агрегатных индексов позволяет получить систему взаимосвязанных индексов и провести анализ влияния отдельных факторов на изменение обобщающих результативных показателей.
Построим индексную модель, отражающую взаимосвязь динамики трех показателей – стоимости продукции, цен и количества реализованной продукции:
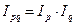 .
.
Такая модель называется мультипликативной.
Мы получили систему взаимосвязанных агрегатных индексов, каждый из которых позволяет определить изменение индексируемого показателя в относительном выражении (%).
Одна из задач индексного метода – анализ влияния отдельных факторов на изучаемое явление. Индексы рассматривают как показатели относительно изменения результативного показателя за счет отдельных факторов.
Общее изменение стоимости продукции в абсолютном выражении исчисляется как разность между числителем и знаменателем общего индекса стоимости реализованной продукции:
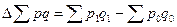 .
.
Исходя из того, что на изменение стоимости продукции оказывают влияние два фактора (количество реализованной продукции и цены), приведем формулы расчета влияния каждого из этих факторов:
· изменение стоимости реализованной продукции в абсолютном выражении за счет изменения цен исчисляется как разница между числителем и знаменателем индекса цен:
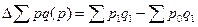 ;
;
· изменение стоимости продукции в абсолютном выражении за счет изменения количества реализованной продукции исчисляется как разность между числителем и знаменателем индекса физического объема продукции:
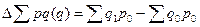 .
.
Взаимосвязь исчисленных показателей:
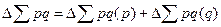 .
.
Задача 1
Имеются следующие данные о продаже продукции:
| Продукция | Базисный период | Отчетный период | ||
| Количество, шт. | Цена, тыс. руб. | Количество, шт. | Цена, тыс. руб. | |
| А | 6,2 | 5,8 | ||
| В | 4,6 | 5,2 | ||
| С | 6,1 | 6,0 |
На основе приведенных данных определить:
1) индивидуальные индексы цен и физического объема;
2) общие индексы цен, физического объема и товарооборота.
3) прирост товарооборота в целом и за счет изменения цен и физического объема.
РЕШЕНИЕ
1) индивидуальные индексы цен (характеризуют изменение цен по отдельным видам продукции)
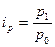 , где р1 – цена отчетного периода,
, где р1 – цена отчетного периода,
р0 –цена базисного периода
А 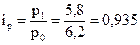 , или 93,5%;
, или 93,5%;
В 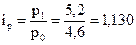 , или 113,0%;
, или 113,0%;
С 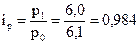 , или 98,4%.
, или 98,4%.
Следовательно, цена на продукцию «В» выросла на 13,0%; по продукции «А» и «С» снизилась на 6,5 и 1,6% соответственно.
Индивидуальные индексы физического объема (характеризуют изменение количества проданных отдельных видов продукции)
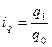 , где q1 – количество продукции отчетного периода,
, где q1 – количество продукции отчетного периода,
q0 – количество продукции базисного периода
А 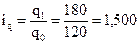 , или 150,0%;
, или 150,0%;
В 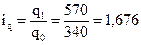 , или 167,6%;
, или 167,6%;
С 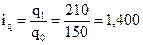 , или 140,0%.
, или 140,0%.
Таким образом, количество проданной продукции «А» выросло в 1,5 раза, продукции «В» – на 67,6%, продукции «С» – на 40,0%.
2) Общий индекс цен (характеризует среднее изменение цен)
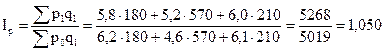 , или 105,0%.
, или 105,0%.
Цены на всю продукцию выросли в среднем на 5,0%.
Общий индекс физического объема
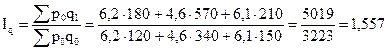 , или 155,7%.
, или 155,7%.
Количество проданной продукции в отчетном периоде по сравнению с базисным выросло на 55,7%.
Общий индекс товарооборота
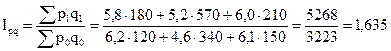 , или 163,5%.
, или 163,5%.
Товарооборот вырос на 63,5%.
Взаимосвязь между исчисленными индексами:
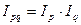
1,635 = 1,050 * 1,557
3) Прирост товарооборота в целом:
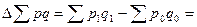 5268 – 3223 = + 2045 тыс. руб.
5268 – 3223 = + 2045 тыс. руб.
а) за счет изменения цен:
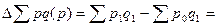 5268 – 5019 = + 249 тыс. руб.
5268 – 5019 = + 249 тыс. руб.
б) за изменения физического объема
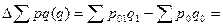 5019 – 3223 = + 1796 тыс. руб.
5019 – 3223 = + 1796 тыс. руб.
Взаимосвязь:
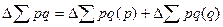
+ 2045 = + 249 + 1796
Вывод: В отчетном периоде по сравнению с базисным товарооборот вырос на 2045 тыс. руб., или на 63,5%; в том числе за счет роста цен товарооборот вырос на 249 тыс. руб., или на 5,0%; за счет увеличения объемов продаж товарооборот вырос на 1796 тыс. руб., или на 55,7%.
Дата добавления: 2016-02-16; просмотров: 1696;
