Средневзвешенные индексы
Помимо агрегатных индексов в статистике применяются средневзвешенные индексы.К их исчислению прибегают тогда, когда имеющаяся в распоряжении информация не позволяет рассчитать общий агрегатный индекс.
Средний индекс - это индекс, вычисленный как средняя величина из индивидуальных индексов. Он должен быть тождествен агрегатному индексу. При исчислении средних индексов используются две формы средних: арифметическая и гармоническая.
При построении средних индексов следует руководствоваться следующим правилом: для индекса количественного показателя обычно используют формулу среднего арифметического индекса, а для индекса качественного показателя – формулу среднего гармонического индекса.
Среднеарифметический индекс физического объема продукции вычисляется по формуле:
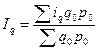 .
.
Среднеарифметические индексы чаще всего применяются на практике для расчета сводных индексов количественных показателей.
Средний гармонический индекс цен представляет собой среднюю гармоническую величину из индивидуальных индексов цен:
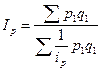 .
.
Имеются данные о продаже товаров в районе
| Товарные группы | Стоимость продажи товаров в 2011 г., млн. руб. | Прирост количества продажи в 2012 г. к 2011 г., % |
| Ткани | +10 | |
| Обувь | +20 | |
| Трикотажные изделия | Без изменения |
Определите:
1) Общий индекс физического объёма товарооборота;
2) Абсолютный прирост стоимости проданных товаров за счёт изменения количества продажи товаров.
Решение:
1) Определим общий индекс физического объёма товарооборота
Ткани:
iq = 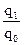 = 1, 1 или 110%
= 1, 1 или 110%
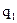 = iq
= iq 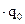
Iq = 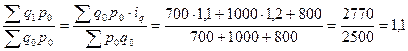 или 110 %
или 110 %
2) Определим абсолютный прирост стоимости проданных товаров за счёт изменения количества продажи товаров (разница между числителем и знаменателем индекса физического объёма товарооборота)
Iq = 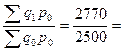 770 – 2500 = 270 млн. руб.
770 – 2500 = 270 млн. руб.
Товарооборот в отчётном периоде по сравнению с базисным возрос на 270 млн. руб.
Индексы в форме средних из индивидуальных используют не только для характеристики изменения цен и физического объема, но и других (в основном, качественных) показателей: себестоимости, производительности труда, рентабельности и т.д. При этом должно выполняться основное требование – их тождественность агрегатному индексу и реальность весов как экономических категорий.
Динамику среднего уровня качественного показателя для однородной совокупности изучают с помощью системы индексов переменного, постоянного состава и структурных сдвигов.
Относительная величина, характеризующая динамику среднего уровня качественного показателя в однородной совокупности, называется индексом переменного состава. Он отражает влияние на изучаемый показатель двух факторов: изменения индексируемой величины у отдельных единиц совокупности и изменения структуры совокупности по изучаемому признаку. Индекс переменного состава для любых качественных показателей может быть построен следующим образом:
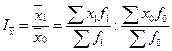 ,
,
где х – индексируемая величина;
f – вес индекса.
Индекс постоянного (фиксированного) состава характеризует динамику среднего уровня качественного показателя при одинаковой фиксированной структуре совокупности. Другими словами, он показывает, как в среднем изменилось значение качественного показателя у единиц совокупности. В общем виде данный индекс можно записать следующим образом:
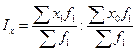 .
.
Индекс влияния структурных сдвигов представляет собой отношение средних величин рассматриваемого качественного показателя, рассчитанных при структуре совокупности отчетного и базисного периодов при постоянном значении качественного показателя. Формула индекса влияния структурных сдвигов:
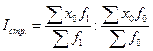 .
.
Влияние структурных сдвигов на изменение среднего уровня изучаемого явления особенно заметно при сравнениях за длительные периоды времени и в условиях существенных изменений в структуре социально-экономических процессов. В связи с этим исключение воздействия структурного фактора при анализе изменений средних значений признаков как показателей основной тенденции – это необходимое условие для получения реалистичной оценки и правильных выводов на основе индексного анализа различных сложных явлений.
Взаимосвязь индексов переменного, постоянного состава и влияния структурных сдвигов выражается уравнением:
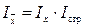
На основе этих формул можно рассчитать абсолютное изменение среднего уровня вторичного признака за счет отдельных факторов – самого усредняемого признака и структуры.
Имеются следующие данные о реализации яблок на рынках города:
| Продукция | Сентябрь | Декабрь | ||
| Количество, кг | Цена, руб. | Количество, кг | Цена, руб. | |
| №1 | ||||
| №2 | ||||
| №3 |
На основе приведенных данных определить для трех рынков вместе:
1) индексы средней цены яблок переменного состава, постоянного состава и структурных сдвигов;
2) абсолютное изменение средней цены яблок по рынкам города в целом и за счет действия отдельных факторов.
РЕШЕНИЕ
1) Индекс переменного состава средней цены равен отношению средней цены отчетного периода к средней цене базисного периода
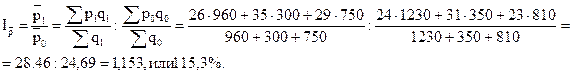
Индекс постоянного состава
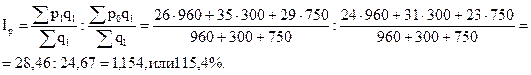
Индекс структурных сдвигов
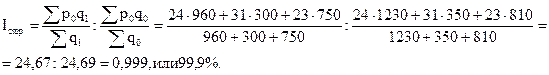
Взаимосвязь индексов:
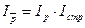 1,153 = 1,154 * 0,999
1,153 = 1,154 * 0,999
2) Абсолютное изменение:
Средней цены:
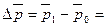 28,46 – 24,69 = + 3,77 руб.
28,46 – 24,69 = + 3,77 руб.
а) за счет изменения цен на отдельных рынках
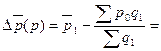 28,46 – 24,67 = + 3,79 руб.
28,46 – 24,67 = + 3,79 руб.
б) за счет изменения в структуре продаж
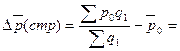 24,67 – 24,69 = – 0,02 руб.
24,67 – 24,69 = – 0,02 руб.
Взаимосвязь: 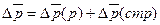
+ 3,77 = + 3,79 – 0,02
Вывод: Средняя цена яблок выросла в декабре по сравнению с сентябрем на 3,77 руб., или на 15,3%, в том числе за счет роста цен на отдельных рынках – на 3,79 руб. За счет изменения структуры продаж средняя цена снизилась на 2 коп.
Дата добавления: 2016-02-16; просмотров: 1666;
