Методы изучения связи социальных явлений
Важной задачей статистики является разработка методики статистической оценки социальных явлений, которая осложняется тем, что многие социальные явления не имеют количественной оценки.
Количественная оценка связей социальных явлений осуществляется на основе расчета и анализа целого ряда коэффициентов.
Коэффициент ассоциации и контингенции.Для определения тесноты связи двух качественных признаков, каждый из которых состоит только из двух групп, применяются коэффициенты ассоциации и контингенции. Для их вычисления строится таблица, которая показывает связь между двумя явлениями, каждое из которых должно быть альтернативным, т.е. состоящим из двух качественно отличных друг от друга значений признака (например, хороший, плохой) (таблица 3).
Таблица 3
Таблица для вычисления коэффициентов
ассоциации и контингенции
| a | b | a + b |
| c | d | c + d |
| a + c | b + d | a + b + c + d |
Коэффициенты вычисляются по формулам:
ассоциации: 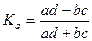 ;
;
контингенции: 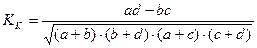 .
.
Коэффициент контингенции всегда меньше коэффициента ассоциации. Связь считается подтвержденной, если Ка > 0,5 или Кк > 0,3. Изменяются от – 1 до + 1.
Пример
Зависимость участия рабочих в забастовках от образовательного уровня
| Группы рабочих | Число рабочих | |
| участвующих в забастовке | не участвующих в забастовке | |
| Окончившие среднюю школу | 78 a | 22 b |
| Не окончившие среднюю школу | 32 c | 68 d |
Определить коэффициент ассоциации
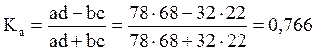
Определить коэффициент контингенции
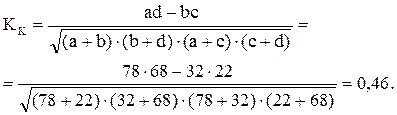
Таким образом, связь между рассматриваемыми признаками не столь существенна.
Когда каждый из качественных признаков состоит более чем из двух групп, то для определения тесноты связи возможно применение коэффициентов взаимной сопряженности Пирсона и Чупрова, которые вычисляются по следующим формулам:
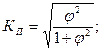
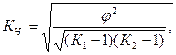
где 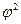 - показатель средней квадратической сопряженности.
- показатель средней квадратической сопряженности.
Показатель 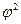 определяется как сумма отношений квадратов частот каждой клетки таблицы к произведению итоговых частот соответствующего столбца и строки за минусом единицы;
определяется как сумма отношений квадратов частот каждой клетки таблицы к произведению итоговых частот соответствующего столбца и строки за минусом единицы;
К1 – число значений (групп) первого признака;
К2 – число значений (групп) второго признака.
Чем ближе значение коэффициентов к 1, тем связь теснее.
Коэффициент взаимной сопряженности Чупрова является более гибким, поскольку он учитывает число образуемых по каждому признаку групп (К1 и К2), поэтому является более точным по сравнению с коэффициентом взаимной сопряженности по формуле Пирсона.
Коэффициент взаимной сопряженности изменяется от 0 до 1.
Пример
С помощью коэффициентов взаимной сопряженности исследовать связь между себестоимостью продукции и расходами на ее реализацию, тыс. руб.
| Расходы на реализацию продукции | Себестоимость продукции | ИТОГО | ||
| Низкая | Средняя | Высокая | ||
| Низкие | ||||
| Средние | ||||
| Высокие | ||||
| ИТОГО |
Коэффициент взаимной сопряженности Пирсона
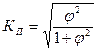
Сначала определим
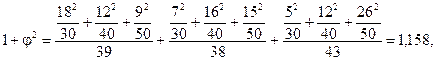
отсюда 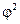 = 1,158 – 1 = 0,158.
= 1,158 – 1 = 0,158.
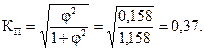
Коэффициент взаимной сопряженности Чупрова
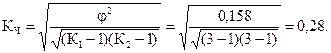
К1 – число значений (групп) первого признака; К2 – число значений (групп)
второго признака
Вывод: связь между расходами на реализацию и себестоимостью продукции слабая.
Дата добавления: 2016-02-16; просмотров: 1243;
