Собственно-корреляционные параметрические методы изучения связи. Оценка существенности корреляции
Изменение тесноты и направления связи является важной задачей изучения количественного измерения взаимосвязи социально-экономических явлений.
Теснота связи при линейной зависимости измеряется с помощью линейного коэффициента корреляции.
В статистической теории разработаны и на практике применяются различные модификации формул расчета данного коэффициента:
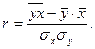
Производя расчет по итоговым значениям исходных переменных, линейный коэффициент корреляции можно вычислить по формуле:
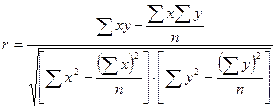
Линейный коэффициент может быть также выражен через дисперсии слагаемых:
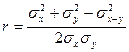 .
.
Между линейным коэффициентом корреляции и коэффициентом регрессии (а1) существует определенная зависимость, которую можно математически выразить следующей формулой:
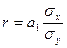 .
.
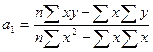 .
.
Линейный коэффициент корреляции изменяется в пределах от – 1 до 1. Знаки коэффициентов регрессии и корреляции совпадают. При этом интерпретацию выходных значений коэффициента корреляции можно представить в таблице 2.
Таблица 2
Оценка линейного коэффициента корреляции
| Значение линейного коэффициента связи | Характер связи | Интерпретация связи |
| r = 0 | Отсутствует | - |
| 0 < r < 1 | Прямая | С увеличением Х увеличивается У |
| -1 < r < 0 | Обратная | С увеличением Х уменьшается У, и наоборот |
| r = 1 | Функциональная | Каждому значению факторного признака строго соответствует одно значение результативного признака |
Значимость линейного коэффициента корреляции проверяется на основе t-критерия Стьюдента:
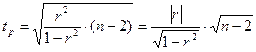 .
.
Если расчетное значение tp > tкр (табличное), то гипотеза Н0: r = 0 отвергается, что свидетельствует о значимости линейного коэффициента корреляции, а следовательно, и о статистической существенности зависимости между х и у.
Пример.Имеются следующие данные о товарообороте и товарных запасах по 8 торговым предприятиям города:
| Номер торгового предприятия | Товарооборот, тыс. руб. | Товарные запасы, тыс. руб. |
Для характеристики зависимости между товарооборотом и товарными запасами рассчитайте:
1) линейный коэффициент корреляции.
2) параметры линейного уравнения корреляционной связи и теоретические (расчетные) уровни товарных запасов.
Решение
1) Теснота связи при линейной зависимости измеряется с помощью линейного коэффициента корреляции.
Линейный коэффициент корреляции можно вычислить по формуле:
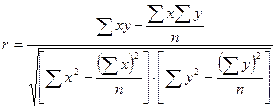 =
=
Для расчета коэффициента корреляции и параметров уравнения необходимо построить вспомогательную таблицу.
Вспомогательная таблица
| № | Товарооборот, тыс. руб. У | Товарные запасы, тыс. руб. Х | ух | х2 | у2 | Ух |
| 251,4 | ||||||
| Итого |
2) Линейная связь может быть выражена уравнением прямой
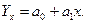
Решая систему нормальных уравнений, определяем параметры а0 и а1:
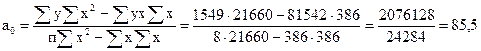
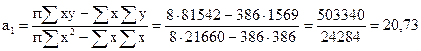
Вид уравнения регрессии: 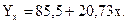
Расчет для каждого значения х:
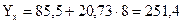
Теснота связи при криволинейной зависимости измеряется с помощью корреляционного отношения. Различают эмпирическое и теоретическое корреляционное отношение. Вычислим эмпирическое корреляционное отношение:
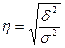 .
.
Вычисленное корреляционное отношение требует достаточно большого объема информации, которая должна быть представлена в форме групповой таблицы или в форме корреляционной таблицы, т.е. обязательным условием является группировка данных по признаку-фактору (изменяется от 0 до 1).
Теоретическое корреляционное отношение рассчитывается по формуле:
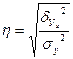 ,
,
где 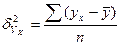 - дисперсия в ряду выравненных значений результативного
- дисперсия в ряду выравненных значений результативного
показателя Ух.
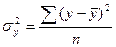 - дисперсия в ряду фактических значений У.
- дисперсия в ряду фактических значений У.
Если 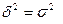 , то это означает, что роль других факторов в вариации у сведена на нет, и отношение η = 1 означает полную зависимость вариации у от х. Если
, то это означает, что роль других факторов в вариации у сведена на нет, и отношение η = 1 означает полную зависимость вариации у от х. Если 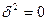 , то это означает, что вариация х никак не влияет на вариацию у, и в этом случае η = 0.
, то это означает, что вариация х никак не влияет на вариацию у, и в этом случае η = 0.
Корреляционное отношение в квадрате называют коэффициентом детерминации (причинности), он отражает долю факторной дисперсии в общей дисперсии.
В практике могут быть использованы и другие показатели для определения степени тесноты связи.
Элементарной характеристикой степени тесноты связи является коэффициент Фехнера:
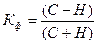 ,
,
где С – количество совпадений знаков отклонений индивидуальных величин факторного признака х и результативного признака у от их средней арифметической величины;
Н – количество несовпадений знаков отклонений индивидуальных значений изучаемых признаков от значения их средней арифметической.
Коэффициент Фехнера целесообразно использовать для установления факта наличия связи при небольшом объеме исходной информации. Он изменяется в пределах -1≤ Кф ≤ 1. При величине Кф = ±1 имеем зависимость признаков, близкую к функциональной. О форме связи – линейная или нелинейная – по величине коэффициента Фехнера ничего определенного сказать нельзя.
Дата добавления: 2016-02-16; просмотров: 1396;
