Простая дисперсия для несгруппированных данных

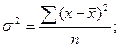
взвешенная дисперсия для вариационного ряда

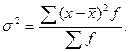
Формулу для расчета можно преобразовать:

,

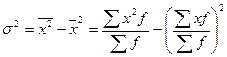т.е. дисперсия равна разности средней из квадратов вариантов и квадрата их средней.

Свойства дисперсии

Свойство 1. Если все значения признака уменьшить или увеличить на одну и ту же постоянную величину А, то дисперсия от этого не изменится.

Свойство 2. Если все значения признака уменьшить или увеличить в одно и то же число раз (i раз), то дисперсия соответственно уменьшится или увеличится в i² раз.

Ø Среднее квадратическое отклонение равно корню квадратному из дисперсии.

.

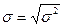Среднее квадратическое отклонение – это обобщающая характеристика размеров вариации признака в совокупности; оно показывает, на сколько в среднем отклоняются конкретные варианты от их среднего значения; является абсолютной мерой колеблемости признака и выражается в тех же единицах, что и варианты, поэтому экономически хорошо интерпретируется.

Дисперсию и среднее квадратическое отклонение используют при расчетах, связанных с организацией выборочного наблюдения, оценке полученных на основе выборки статистических показателей, построении показателей тесноты корреляционной связи, дисперсионном анализе. В условиях нормального распределения существует следующая зависимость между величиной среднего квадратического отклонения и количеством наблюдений: в пределах 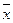± 1σ располагается 0,683 количества наблюдений, 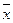± 2σ – 0,954; 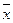± 3σ – 0,997.

Отклонение 3σ можно считать максимально возможным. Это положение называют правилом «трех сигм».

Относительной мерой колеблемости признака является коэффициент вариации.

Ø Коэффициент вариации представляет собой выраженное в процентах отношение среднего квадратического отклонения к средней арифметической:

.

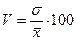Коэффициент вариации используют не только для сравнительной оценки вариации единиц совокупности, но и как характеристику однородности совокупности. Совокупность считается количественно однородной, если коэффициент вариации не превышает 33 %.

Пример. Рассчитать показатели вариации для дискретного ряда (несгруппированных данных), если известна выработка двух бригад строителей по одному виду продукции. Данные представлены во вспомогательной табл. 4.1.

Таблица 4.1

№ п/п	Выработка в дет.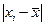
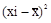
1 бриг.	2 бриг.	1 бриг.	2 бриг.	1 бриг.	2 бриг.
Итого

а) Абсолютные показатели вариации:

Размах вариации: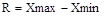

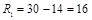деталей;

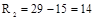деталей.

Отклонение крайних вариант выработки в I бригаде на две детали выше, чем во второй (16–14).

Для нахождения остальных показателей вариации необходимо найти среднюю выработку по каждой бригаде. Определяем среднюю выработку по средней арифметической простой:

;

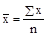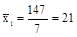деталь; 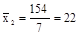детали;

среднее линейное отклонение:

;

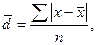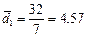деталей; 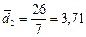деталей.

Степень рассеивания признаков в 1-й бригаде выше, чем во 2-й.

Дисперсия(средний квадрат отклонений) и среднее квадратическое отклонение для несгруппированных данных рассчитываются по следующим формулам:

; ;

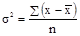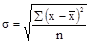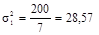деталей; 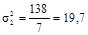деталей;

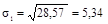деталей; 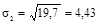детали.

Среднее квадратическое отклонение по величине всегда больше среднего линейного отклонения. Соотношение 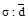для нормального закона распределения должно равняться примерно 1:2.

В задаче соотношение ; .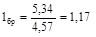

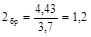Следовательно, резких выделяющихся отклонений не однородных с основной массой элементов не наблюдается.

б) Относительные показатели вариации:

коэффициент осцилляции или относительный размах вариации:

.

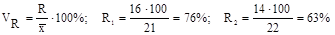Колеблемость крайних показателей выработки вокруг средней в 1-й бригаде больше, чем во 2-й.

Линейный коэффициент вариации (относительное линейное отклонение):

.

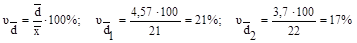Доля усредненных значений абсолютных отклонений от средней в 1-й бригаде выше, чем во 2-й на четыре процента (21–17).

Коэффициент вариации:

.

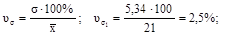
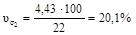Так как коэффициент вариации < 33%, совокупности считаются однородными.

в) Расчет показателей вариации для интервального вариационного ряда представлен в табл. 4.2.

4.4.2. Имеется распределение предприятий по объему выпуска продукции:

Таблица 4.2

Группы предприя­тий по выпуску про­дукции (х), млн руб.	Число предпри­ятий f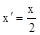
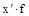
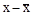
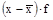
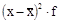
До 2				3,8	7,6	28,88
2–4				1,8	9,0	16,2
4–6				0,2	1,6	0,32
6–8				2,2	6,6	14,52
8–10				4,2	8,4	35,28
Итого:		-		-	33,2	95,2

1) 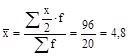млн руб.

2) 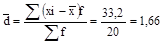млн руб.

3) 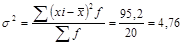млн руб.

4) 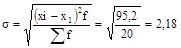млн руб.

5) .

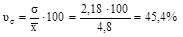Следовательно, вариация групп предприятий по выпуску продукции неоднородная, т.к. коэффициент вариации больше 33% и составляет 45,4 %.