Формулы расчета различных видов степенных средних
| Значение m | Наименование средней | Формулы средней | |
| простая | взвешенная | ||
| при m= -1 | средняя гармоническая | 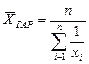
| 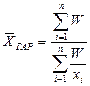
|
| при m = 0 | средняя геометрическая | 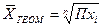
| 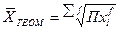
|
| при m = 1 | средняя арифметическая | 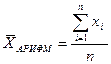
| 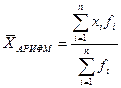
|
| при m = 2 | средняя квадратическая | 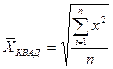
| 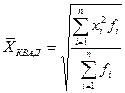
|
Чем больше m (показатель степени), тем больше и величина соответствующей средней.
Следующий пример показывает, что разные виды средних при одном и том же исходном материале имеют неодинаковое значение:
Продолжительность стажа, лет, 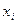
| 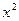
| 1/x | ||
| 1/3 1/6 | ||||
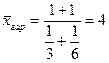 года;
года; 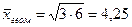 года;
года;
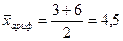 года;
года; 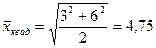 года;
года;
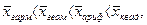
что называется мажорантностью средних.
Все средние, за исключением средней агрегатной, могут рассчитываться в двух вариантах – как взвешенные или невзвешенные.
Средняя арифметическая простая, которая применяется в случаях, если каждая варианта встречается по одному или одинаковому числу раз. Она равна сумме отдельных значений осредняемого признака, деленной на общее число этих значений (она применяется в тех случаях, когда имеются несгруппированные индивидуальные значения признака):
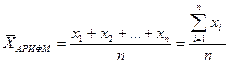 ,
,
где 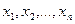 - индивидуальные значения варьирующего признака (варианты);
- индивидуальные значения варьирующего признака (варианты);
п – число единиц совокупности.
Средняя из вариантов, которые повторяются различное число раз, или, как говорят, имеют различный вес, называется взвешенной. В качестве весов выступают численности единиц в разных группах совокупности (в группу объединяют одинаковые варианты).
Средняя арифметическая взвешенная – средняя сгруппированных величин 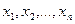 , - вычисляется по формуле:
, - вычисляется по формуле:
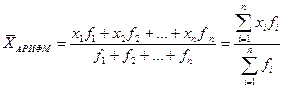 ,
,
где 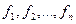 - веса (частоты повторения одинаковых признаков);
- веса (частоты повторения одинаковых признаков);
Σxf – сумма произведений величины признаков на их частоты;
Σf – общая численность единиц совокупности.
В отдельных случаях веса могут быть представлены не абсолютными величинами, а относительными (в % или долях единицы). Тогда формула средней арифметической взвешенной будет иметь вид:
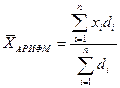 ,
,
где 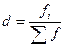 частость, т.е. доля каждой частоты в общей сумме всех частот.
частость, т.е. доля каждой частоты в общей сумме всех частот.
Если частоты рассчитываются в долях (коэффициентах), то Σd=1 и формула имеет вид: 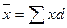 .
.
Средняя арифметическая величина может быть дробным числом, если даже индивидуальные значения принимают только целые значения (дискретный признак). Ничего «предосудительного» для метода средних в этом не заключено; из сущности средней не вытекает, что она обязана быть реальным значением признака, которое могло бы встретиться у какой-либо единицы совокупности.
Если значения осредняемого признака заданы в виде интервалов («от – до»), т.е. интервальных рядов распределения, то при расчете средней арифметической величины в качестве значений признаков в группах принимают середины этих интервалов, в результате чего образуется дискретный ряд. При этом величины открытых интервалов (первый и последний) условно приравниваются к интервалам, примыкающим к ним (второй и последний).
При таком исчислении допускается некоторая неточность, поскольку делается предположение о равномерности распределения единиц признака внутри группы. Однако ошибка будет тем меньше, чем уже интервал и чем больше единиц в интервале.
Свойства средней арифметической:
Свойство 1. Если все индивидуальные значения признака (т.е. все варианты) уменьшить или увеличить в i раз, то среднее значение нового признака соответственно уменьшится или увеличится в i раз.
Свойство 2. Если все варианты осредняемого признака уменьшить или увеличить на число А, то средняя арифметическая соответственно уменьшится или увеличится на это же число А.
Свойство 3. Если веса всех осредняемых вариантов уменьшить или увеличить в k раз, то средняя арифметическая не изменится.
Любая средняя величина должна исчисляться так, чтобы при замене ею каждого варианта осредняемого признака не изменялся итоговый, обобщающий, или, как его принято называть, определяющий показатель, который связан с осредняемым показателем (например, при замене фактических заработных плат отдельных работников предприятия средней заработной платой, не должен измениться фонд заработной платы). Следовательно, в каждом конкретном случае в зависимости от характера имеющихся данных существует только одно истинное среднее значение показателя, адекватное свойствам и сущности изучаемого социально-экономического явления.
В тех случаях, когда вес каждого варианта равен единице (индивидуальное значение обратного признака встречается по одному разу), применяется средняя гармоническая простая:
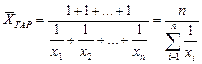 ,
,
где 1/х – отдельные варианты обратного признака, встречающиеся по одному разу; п – число вариантов.
Если в исходном соотношении, из которого определяется средняя, известно произведение варианты на частоту и отдельные варианты, отсутствуют сведения о частотах, то для расчета средней применяется средняя гармоническая взвешенная:
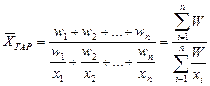 , W= X·f; f = W / X.
, W= X·f; f = W / X.
Средняя гармоническая применяется тогда, когда неизвестны действительные веса f, а известно w = xf, т.е. в тех случаях, когда средняя предназначается для расчета сумм слагаемых, обратно пропорциональных величине данного признака, когда суммированию подлежат не сами варианты, а обратные им величины.
| Решение типовых задач | |||||||||||||||||||||||||||||||||
1. Известны данные о заработной плате бригады строителей по профессиям.
Таблица 1
Определите среднюю заработную плату рабочих по профессии и в целом по бригаде. | |||||||||||||||||||||||||||||||||
| Решение: | |||||||||||||||||||||||||||||||||
Исчислим среднюю заработную плату для монтажников. В данном случае веса (частоты) равны единице, следовательно, расчет средней заработной платы монтажников произведем по формуле средней арифметической простой:
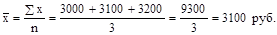 Если в рядах распределения веса (частоты) равны между собой (слесари-сантехники), то расчет производится тоже по формуле средней арифметической простой.
Следовательно, средняя заработная плата слесарей-сантехников будет равна:
Если в рядах распределения веса (частоты) равны между собой (слесари-сантехники), то расчет производится тоже по формуле средней арифметической простой.
Следовательно, средняя заработная плата слесарей-сантехников будет равна:
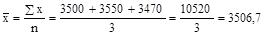 руб.
Если же частоты имеют различные количественные значения (сварщики), то средняя заработная плата определяется по формуле средней арифметической взвешенной: руб.
Если же частоты имеют различные количественные значения (сварщики), то средняя заработная плата определяется по формуле средней арифметической взвешенной:
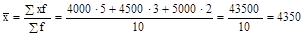 руб.
Средняя заработная плата рабочих по бригаде строителей может быть определена двумя способами:
1) как средняя арифметическая взвешенная из групповых средних: руб.
Средняя заработная плата рабочих по бригаде строителей может быть определена двумя способами:
1) как средняя арифметическая взвешенная из групповых средних:
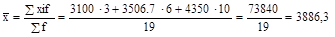 руб.;
2) как отношение фонда оплаты по группам профессий к общей численности рабочих этих групп: руб.;
2) как отношение фонда оплаты по группам профессий к общей численности рабочих этих групп:
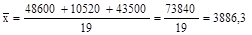 руб.
2. Имеются сведения о ценах реализации мяса на ярмарке города в базисном и отчетном периодах.
Таблица 2 руб.
2. Имеются сведения о ценах реализации мяса на ярмарке города в базисном и отчетном периодах.
Таблица 2
Определить среднюю цену реализации мяса в базисном и отчетном периоде. | |||||||||||||||||||||||||||||||||
| Решение | |||||||||||||||||||||||||||||||||
Средняя цена в базисном периоде определяется из экономического содержания по формуле средней арифметической взвешенной:
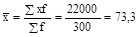 руб.
В отчетном периоде известна выручка и цена, количество товара неизвестно. Для получения количества проданного мяса нужно выручку разделить на цену, а затем всю выручку разделить на полученный результат. Таким образом, в нашем примере необходимо использовать среднюю гармоническую взвешенную: руб.
В отчетном периоде известна выручка и цена, количество товара неизвестно. Для получения количества проданного мяса нужно выручку разделить на цену, а затем всю выручку разделить на полученный результат. Таким образом, в нашем примере необходимо использовать среднюю гармоническую взвешенную:
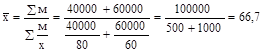 руб.
3. Имеются данные о возрастном составе студентов дистанционной формы обучения по одному из отделений края: 19, 35, 36, 28, 26, 38, 34, 22, 28, 30, 32, 23, 25, 33, 27, 24, 30, 32, 28, 25, 29, 26, 31, 24, 29, 27, 32, 26, 29, 27.
Для анализа распределения студентов дистанционной формы обучения требуется:
1) построить интервальный ряд распределения;
2) дать графическое изображение ряда;
3) исчислить показатели центра распределения, сформировать вывод. руб.
3. Имеются данные о возрастном составе студентов дистанционной формы обучения по одному из отделений края: 19, 35, 36, 28, 26, 38, 34, 22, 28, 30, 32, 23, 25, 33, 27, 24, 30, 32, 28, 25, 29, 26, 31, 24, 29, 27, 32, 26, 29, 27.
Для анализа распределения студентов дистанционной формы обучения требуется:
1) построить интервальный ряд распределения;
2) дать графическое изображение ряда;
3) исчислить показатели центра распределения, сформировать вывод.
| |||||||||||||||||||||||||||||||||
| Решение | |||||||||||||||||||||||||||||||||
1. Для построения интервального ряда определим величину интервала группировки: 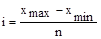 ; n – примем равным 5. ; n – примем равным 5.
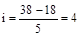 года.
Таблица 3.4
Интервальный ряд распределения года.
Таблица 3.4
Интервальный ряд распределения
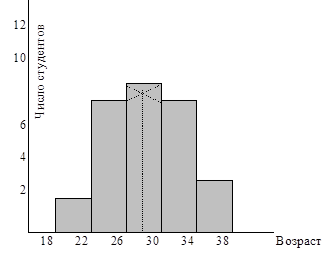
2. Графически вариационный интервальный ряд может быть представлен в виде гистограммы, полигона, кумуляты. Гистограмма, полигон и кумулята строятся в прямоугольной системе координат. На рис. 3.1 представлены гистограмма и полигон распределения. Для преобразования гистограммы в полигон распределения середины верхних сторон прямоугольников соединяют отрезками прямой, и две крайние точки прямоугольников замыкаются по оси абсцисс на середине интервалов.
Рис. 3.1. Гистограмма, полигон распределения студентов по возрасту На основе построенной гистограммы графически можно определить моду. Для этого правую вершину модального прямоугольника соединяют прямой с правым углом предыдущего прямоугольника, а левую вершину модального прямоугольника соединяют с левым углом последующего прямоугольника. Абсцисса точки пересечения этих прямых и будет модой распределения. М0=28 лет. Для графического определения медианы используется кумулята (рис. 3.2). Кумулята строится по накопленным частотам (см. интервальный ряд распределения), Ме»28,5 года. 3. Расчет показателей центра распределения: где х¢ – среднее значение признака в интервале или центр интервала Средний возраст студентов дистанционного обучения 28 лет.
Рис. 3.2. Кумулята распределения студентов Найдем структурные средние М0 и Ме:
Значение полученной моды по формуле соответствует значению моды, полученной на графике.
Графики Ме = 28,5, точнее на графике трудно указать. |
Структурные (позиционные) средние применяются для изучения внутреннего строения и структуры рядов распределения значений признака. К таким показателям относятся мода и медиана.
Мода – наиболее часто встречающаяся величина признака.
Мода – значение случайной величины, встречающееся с наибольшей вероятностью в дискретном вариационном ряду – вариант, имеющий наибольшую частоту.
В интервальных вариационных рядах мода определяется приближенно по формуле:
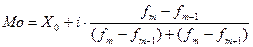 ,
,
где: Мо – модальная величина;
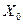 - начальная граница модального интервала;
- начальная граница модального интервала;
i – модальный интервал; определяется по наибольшей частоте.
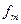 - частота модального интервала;
- частота модального интервала;
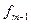 - частота интервала, предшествующая модальному интервалу;
- частота интервала, предшествующая модальному интервалу;
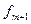 - частота интервала, следующая за модальным интервалом.
- частота интервала, следующая за модальным интервалом.
Медиана –величина признака, находящаяся в середине вариационного ряда, расположенного в порядке возрастания или убывания. Медиана делит ряд на две равные (по числу единиц) части – со значениями признака меньше медианы и со значениями признака больше медианы.
В ранжированных рядах[1] несгруппированных данных нахождение медианы сводится к отысканию порядкового номера медианы.
Пусть ряд состоит из показателей заработной платы 9 рабочих, руб.в месяц:
5500 6300 7000 7500 8000 8200 9100 10 000 12 000.
Номер медианы для нечетного объема вычисляется по формуле:
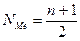 ,
,
где п – число членов ряда.
В нашем примере номер медианы равен 5, медиана равна 8000 руб. (т.е. одна половина рабочих получила зарплату менее 8000 руб., а другая – более 8000 руб. в месяц).
В случае четного объема ряда медиана равна средней из двух вариантов, находящихся в середине ряда (из предыдущего примера: (1100 + 1250):2 = 1175 руб.).
В интервальном вариационном ряду медиана рассчитывается по следующей формуле:
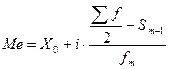 ,
,
где 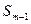 - сумма накопленных частот, предшествующая медианному интервалу.
- сумма накопленных частот, предшествующая медианному интервалу.
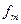 - число наблюдений (частота) в медианном интервале.
- число наблюдений (частота) в медианном интервале.
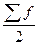 - половина от общего числа наблюдений.
- половина от общего числа наблюдений.
Медианным является первый интервал, в котором сумма накопленных частот превысит половину общего числа наблюдений.
Моду и медиану можно определить графически.
Медиана определяется по кумуляте. Для ее определения высоту наибольшей ординаты, которая соответствует общей численности, делят пополам. Через полученную точку проводят прямую, параллельную оси абсцисс, до пересечения ее с кумулятой. Абсцисса точки пересечения является медианой.
Мода определяется по гистограмме распределения. Для этого правую вершину модального прямоугольника соединяют с правым верхним углом предыдущего прямоугольника, а левую вершину – с левым верхним углом последующего прямоугольника. Абсцисса точки пересечения этих прямых и будет модой.
Соотношение моды, медианы и средней арифметической указывает на характер распределения признака в совокупности, позволяет оценить его асимметрию. Если 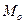 <
< 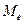 <
< 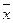 , то имеет место правосторонняя асимметрия ряда, при
, то имеет место правосторонняя асимметрия ряда, при 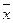 <
< 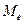 <
< 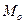 она будет левосторонней.
она будет левосторонней.
Дата добавления: 2016-02-16; просмотров: 1679;

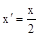
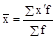 ,
,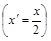 =
= 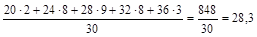 года
года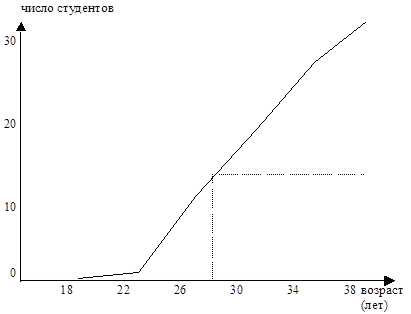
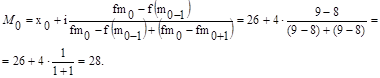

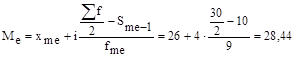 года.
года.