Формулы Бернулли, Лапласа и Пуассона

Формула Бернулли. Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события равна р (0<p<1), событие наступит равно k раз (безразлично в какой последовательности), равна

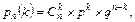где .

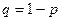При больших n эта вероятность может быть приближенно вычислена по формуле Лапласа:

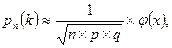где .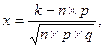

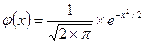Значения функции φ(x) для положительных х затабулированы, а для отрицательных х следует воспользоваться четностью функции: φ(-x)= φ(x).

Если n велико, а вероятность появления события близка к нулю, то большую точность вычисления дает приближенная формула Пуассона:

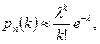где .

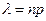Интегральная теорема Лапласа. Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события равна p (0<p<1), событие наступит не менее k₁ раз и не более k₂ раз, приближенно равна

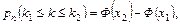где

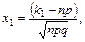
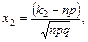
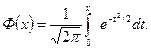
Интегральная функция Лапласа Ф(x) затабулирована для x>0, при x<0 следует использовать свойство нечетности функции Ф(-x)=Ф(x).

Пример 48. В каждом из 700 независимых испытаний событие А происходит с постоянной вероятностью 0.35. Найти вероятность того, что событие А произойдет: а) 270 раз; б) не менее 230 и не более 270 раз; в) не менее 270 раз.

Решение. По условию задачи n=700; p=0.35; q=0.65. Поскольку n достаточно велико, воспользуемся приближенными формулами Лапласа.

а) k=270. Найти P₇₀₀(270).

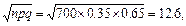
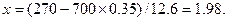
По таблице находим:

.

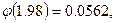
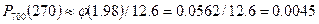б) k₁=230, k₂=270. Найти P₇₀₀(230≤k≤270).

.

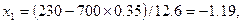
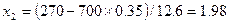Значения Ф(x) найдем по таблице:

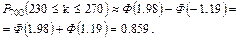
в) k≥270. Найти P₇₀₀(270≤k≤700).

.

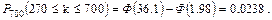Пример 49. Вероятность поражения мишени при одном выстреле равна 0.4. Найти вероятность того, что при 4 выстрелах мишень будет поражена: а) 3 раза; б) не менее 3 раз; в) хотя бы один раз.

Решение. По условию n=4; p=0.4; q=0.6.

а)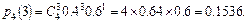

б) .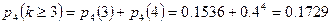

в) .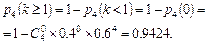

Пример 50. На телефонной станции неправильное соединение происходит с вероятностью 0,005. Найти вероятность того, что среди 200 соединений произойдет: а) одно неправильное соединение; б) меньше 3 неправильных соединений; в) больше 2 неправильных соединений.

Решение. Вероятность рассматриваемого события мала, поэтому воспользуемся формулой Пуассона. По условию n=200, λ=np=200*0.05.

а) k=1, Найти: P₂₀₀(1).

По формуле Пуассона:

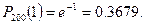
б) k<3. Найти: P₂₀₀ (0≤k<3).

P₂₀₀ (0≤k<3)=P₂₀₀ (0)+ P₂₀₀(1)+ P₂₀₀ (2)=e^-1 (1+1+0,5)=0,9197.

в) k>2. Найти: P₂₀₀ (k>2).

Эту задачу проще решить, если перейти к противоположным событиям.

P₂₀₀ (k>2)=1- P₂₀₀ (k≤2)=1-( P₂₀₀ (0)+ P₂₀₀ (1)+ P₂₀₀ (2))=

=1-P₂₀₀ (k<3)=1-0,9197=0,0803.

51. Два равносильных противника играют в шахматы. Что вероятнее: а) выиграть одну партию из двух или две партии из четырех? б) выиграть не менее двух партий из четырех или не менее трех партий из пяти? Ничьи во внимание не принимаются.

52. Устройство состоит из трех независимо работающих основных элементов. Устройство отказывает, если откажет хотя бы один элемент. Вероятность отказа каждого элемента за время t равна 0,1. Найти вероятность безотказной работы устройства за время t если:

а) работают только основные элементы;

б) включен один резервный элемент;

в) включены два резервных элемента.

Предполагается, что резервные элементы работают в том же режиме, что и основные, вероятность отказа каждого резервного элемента также равна 0,1 и устройство отказывает, если работает менее трех элементов.

53. В семье пять детей. Найти вероятность того, что среди этих детей: а) два мальчика; б) не более двух мальчиков; в) более двух мальчиков; г) не менее двух и не более трех мальчиков. Вероятность рождения мальчика принять равной 0,51.

54. Вероятность поражения мишени при одном выстреле равна 0,8. Найти вероятность того, что при 100 выстрелах мишень будет поражена ровно 75 раз.

55. Вероятность появления события в каждом из 2100 независимых испытаний равна 0,7. Найти вероятность того, что событие появится: а) не менее 1470 и не более 1500 раз; б) не менее 1470 раз; в) не более 1469 раз.

56. Вероятность появления события в каждом из независимых испытаний равна 0,8. Сколько нужно произвести испытаний, чтобы с вероятностью 0,9 можно было ожидать, что событие появится не менее 75 раз?

57. Станок-автомат штампует детали. Вероятность того, что изготовленная деталь окажется бракованной, равна 0,01. Найти вероятность того, что среди 200 деталей окажется ровно 4 бракованных.

58. Магазин получил 1000 бутылок минеральной воды. Вероятность того, что при перевозке бутылка окажется разбитой, равна 0,003. Найти вероятность того, что магазин получит разбитых бутылок: а) ровно две; б) менее двух; в) более двух; г) хотя бы одну.

59. Изготовитель радиоэлектронного оборудования закупает 1000 интегральных микросхем, каждая из которых с вероятностью 0,01 может оказаться неисправной. Какова вероятность того, что

а) неисправны будут ровно 10 микросхем?

б) все микросхемы окажутся исправными?

в) из всех микросхем неисправна будет лишь одна?