Теоремы сложения и умножения вероятностей

Теорема сложения вероятностей совместных событий.Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления:

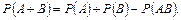
Если события несовместны, то P(AB)=0 и формула принимает вид:

Теорема умножения вероятностей. Вероятность совместного появления двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие произошло:

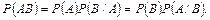
Если события независимы, то P(B/A)=P(B) и формула принимает вид:

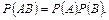
Пример 16. В первой урне 6 белых и 4 черных шара, а во второй – 5 белых и 7 черных шара. Из первой урны случайно взяли 3 шара, а из второй – 2 шара. Найти вероятность того, что среди вынутых шаров:

1) все шары одного цвета;

2) только 3 белых шара;

3) хотя бы один белый шар;

Решение. Шары вынимают из обеих урн независимо. Элементарными событиями будут сочетания по 3 шара из 10 или по 2 из 12. Введем обозначение событий: A₁ – все вынутые шары одного цвета, А₂ – среди извлеченных шаров только 3 белых, А₃ – среди извлеченных шаров имеется хотя бы один белый.

Пусть из первой урны извлечены: В₁ – 3 белых шара, В₂ – 2 белых и один черный, В₃ – 1 белый и 2 черных, В₄ – 3 черных шара. Из второй урны извлечены: D₁ – 2 белых шара, D₂ – 1 белый и 1 черный шар, D₃ – 2 черных шара.

1) Найдем P(A₁). Для этого выразим событие A₁ через B_i и D_k: A₁=B₁D₁+ B₄D₃. События B_i и D_k независимы, а B₁D₁ и B₄D₃ – несовместны, поэтому

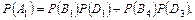
Количество элементарных равновозможных исходов для первой и второй урны соответственно равны:

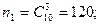
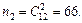
Найдем количество благоприятных исходов для событий B_i, D_k:

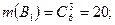
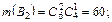
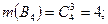
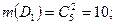
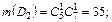
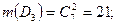
Следовательно:

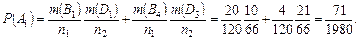
2) A₂=B₁D₃+B₂D₂+B₃D₁.

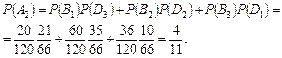
3) Для отыскания P(A₃) введем противоположное событие 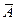₃: среди извлеченных шаров нет белых. Тогда Р( 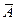₃ ) ,

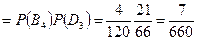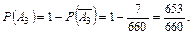
Пример 17. Устройство состоит из трех элементов, работающих независимо. Вероятности безотказной работы (за время t) первого, второго и третьего элементов соответственно равны 0.6; 0.7; 0.8. Найти вероятности того, что за время t безотказно будут работать:

1) только один элемент;

2) только два элемента;

3) все три элемента;

Решение. Введем обозначения событий: A₁ – безотказно работает только один элемент, А₂ – только два, А₃ – все три, В – безотказно работает первый элемент, С – работает второй, D – работает третий. По условию задачи P(B)=0.6; P(C)=0.7; P(D)=0.8.

1) A₁=B 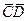+С 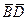+ 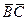D. Тогда:

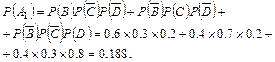
2) A₂=BC 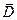+B D+ CD,

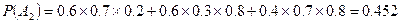
3) A₃=BCD,

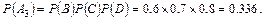
Пример 18. В условиях предыдущей задачи найти вероятность того, что безотказно будут работать:

1) хотя бы 2 элемента;

2) хотя бы 1 элемент;

Решение. Пусть событие Е – работают хотя бы 2 элемента, К – работает хотя бы 1 элемент.

1) E=A₂+A₃,

.

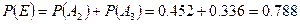2) Введем противоположное событие k̅ - отказали все три элемента. Тогда:

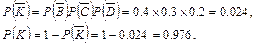
Пример 19. Опыт состоит в последовательном бросании двух монет. Рассматриваются события: А – выпадение герба на первой монете; D – выпадение хотя бы одного герба; E – выпадение хотя бы одной цифры; F – выпадение герба на второй монете. Определить, зависимы или независимы пары событий: 1) A и E, 2) A и F, 3) D и E, 4) D или F.

Решение. Для независимых событий условная вероятность равна безусловной, а для зависимых – они не равны. Выпишем все исходы испытания: г, г; г, ц; ц, г; ц, ц и определим в каждом случае безусловные и условные вероятности.

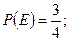
1) 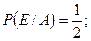события зависимы.

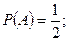
2) 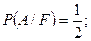события независимы.

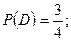
3) 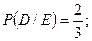события зависимы.

4) 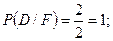события зависимы.

20. Для сигнализации об аварии установлены два независимо работающих сигнализатора. Вероятность того, что при аварии сигнализатор сработает, равна 0,95 для первого сигнализатора и 0,9 для второго. Найти вероятность того, что при аварии сработает только один сигнализатор.

21. Отдел технического контроля проверяет изделия на стандартность. Вероятность того, что изделие стандартно, равна 0,9. Найти вероятность того, что из двух проверенных изделий только одно стандартное.

22. Вероятности того, что нужная сборщику деталь находится в первом, втором, третьем, четвертом ящике, соответственно равны 0,6; 0,7; 0,8; 0,9. Найти вероятности того, что деталь содержится: а) не более чем в трех ящиках; б) не менее чем в двух ящиках.

23. Студент знает 20 из 25 вопросов программы. Найти вероятность того, что студент знает предложенные ему экзаменатором три вопроса.

24. Устройство содержит два независимо работающих элемента. Вероятности отказа элементов соответственно равны 0,05 и 0,08. Найти вероятности отказа устройства, если для этого достаточно, чтобы отказал хотя бы один элемент.

25. Вероятность попадания в мишень каждым из двух стрелков равна 0,3. Стрелки стреляют по очереди, причем каждый должен сделать по два выстрела. Попавший в мишень первым получает приз. Найти вероятность того, что стрелки получат приз.

26. Вероятность хотя бы одного попадания в цель при четырех выстрелах равна 0,9984. Найти вероятность попадания в цель при одном выстреле.

27. При одном цикле обзора радиолокационной станции, следящей за космическим объектом, объект обнаруживается с вероятностью p. Обнаружение объекта в каждом цикле происходит независимо от других. Найти вероятность того, что при n циклах объект будет обнаружен.

28. Имеется m радиолокационных станций, каждая из которых за один цикл обзора обнаруживает объект с вероятностью p (независимо от других циклов и других станций). За время T каждая станция успевает сделать n циклов. Найти вероятности следующих событий: А – объект будет обнаружен хотя бы одной из станций, В – объект будет обнаружен каждой станцией.

29. Завод выпускает радиолампы, каждая лампа может с вероятностью p иметь дефект. После изготовления лампы проверяются последовательно 3 контролерами: первый контролер обнаруживает имеющийся дефект с вероятностью P₁, второй и третий с вероятностью P₂ и P₃. В случае обнаружения дефекта изделие бракуется. Определить вероятность событий: А – изделие будет забраковано, В – изделие будет забраковано вторым контролером, С – изделие будет забраковано всеми контролерами.

30. В технической системе некоторые узлы дублированы. Схемы дублирования узлов и их надежности указаны на рисунках. Определить надежность Р системы.

31. Пусть пространство S = {1, 3, 5, 7, 9, 11} и три его подмножества:

А = {1, 3, 5}, В = {7, 9, 11} и С = (1, 3, 9, 11}. Найдите

A U В А∩В A∩B ∩С 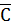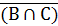A — В

B U C A∩С 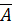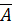∩B A — С (A — В) U В

A U C В∩С 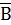A∩ 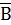С — А (А — В) U С

32. Используя операции над множествами, докажите справедливость следующих выражений:

а) А U (А ∩ В) = А,

б) A U (B ∩ C) = (A U B) ∩ (A U C)_,

в) А U (А ∩ В)=А U В,

г) (A∩B) U (A ∩ B) U (A ∩ B) = A.

33. Пусть каждому элементу введенных в задаче 31 пространства и подпространств соответствует вероятность 1/6. Найдите следующие вероятности:

а) Р(A), б) Р(B), в)Р(С), г) Р(A U B), д) Р(A U C), е) Р ((A — С) U B).

34. Два полупроводниковых диода соединены последовательно. Вероятность короткого замыкания каждого из них составляет 0,05, а обрыва — 0,1. Если считать, что неисправность, возникшая в одном диоде, не влияет па работу другого, то какова вероятность работоспособности цепи?