Дискретных случайных величин
Законом распределения дискретной случайной величины называют перечень её возможных значений и соответствующих им вероятностей. Он может быть в виде таблицы, называемой рядом распределения, первая строка которой содержит возможные значения xi, а вторая- вероятность Pi их появления:
| xi | x1 | x2......... | xn |
| Pi | P1 | P2......... | Pn |
где 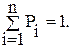
Если множество возможных значений X бесконечно (счётно), то ряд p1+p2+…pn+… сходится и его сумма равна 1.
Математическим ожиданием дискретной случайной величины называют сумму произведений всех её возможных значений на вероятности их появления:
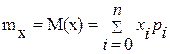
Математическое ожидание обладает следующими свойствами:
1) M(C)=C;
2) M(CX)=CM(X);
3) 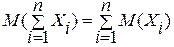
4) Для взаимно независимых случайных величин:
M(X1X2…Xn)= M(X1) M(X2) M(X3)…M(Xn).
Дисперсией случайной величины X называют математическое ожидание квадрата отклонения случайной величины от её математического ожидания:
Д[X]=M[X-M(X)]2.
Дисперсия обладает следующими свойствами:
1) Д(X)=M(X2)-[M(X)]2;
2) Д(C)=0;
3) Д(CX)=C2 Д(X), где С- постоянная величина.
Для независимых случайных величин:
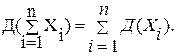
Средним квадратическим отклонением случайной величины называют квадратный корень из её дисперсии:
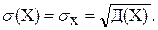
Пример 60. Для проведения технологических испытаний из партии в 100 радиоэлектронных блоков, среди которых имеется 10 неисправных, взяты 5 блоков. Построить ряд распределения случайного числа X бракованных блоков в выборке.
Решение. Число бракованных блоков в выборке может быть любым числом в пределах от 0 до 5, поэтому частные значения xi случайной величины X равны: х1 = 0; х2 =1; х3 = 2; х4 = 3; х5 = 4; х 6 = 5.
Общее число возможных элементарных исходов испытаний равно числу способов, которыми можно извлечь n блоков из N, т. е. равно числу сочетаний из N элементов по п: 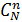 . Среди п блоков d - бракованные. Из Q бракованных блоков можно взять d блоков
. Среди п блоков d - бракованные. Из Q бракованных блоков можно взять d блоков 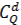 способами, при этом остальные n - d блоков будут годными. Выбрать же п - d годных блоков из п - Q годных можно
способами, при этом остальные n - d блоков будут годными. Выбрать же п - d годных блоков из п - Q годных можно 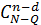 способами. Следовательно, число благоприятных исходов равно
способами. Следовательно, число благоприятных исходов равно 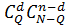 .
.
Искомая вероятность равна отношению числа благоприятных исходов к числу всех элементарных исходов:
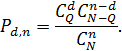
В нашем случае N = 100, Q = 10, п = 5, тогда вероятность того, что в выборке окажется d бракованных радиоэлектронных блоков (P = 0,1, 2, 3, 4, 5), равна
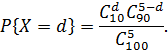
В результате расчетов по этой формуле с точностью до 0,001 получим
P 1 =Р{ X =0} = 0,583; P2 =Р{ X =1} = 0,340; P 3 =Р{ X = 2} = 0,070; P 4 =Р{ X =3} = 0,007; P5 =Р{ X =4} =0, P6 =Р{ X =5} =0.
По результатам расчета выписываем ряд распределения:
xL 0 1 2 3 4 5
Pdtn 0,583 0,340 0,070 0,007 0 0
Пример 57. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение дискретной случайной величины X, заданной законом распределения:
| xi | -5 | |||
| Pi | 0,4 | 0,3 | 0,1 | 0,2 |
Решение. Найдем математическое ожидание и дисперсию. Все промежуточные вычисления удобно внести в таблицу:
| xi | -5 | ∑ | |||
| Pi | 0,4 | 0,3 | 0,1 | 0,2 | |
| xi*Pi | -2 | 0,6 | 0,3 | 0,8 | -0,3 |
| xi2 | |||||
| xi2*Pi | 1,2 | 0,9 | 3,2 | 15,3 |
Тогда получаем:
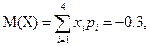
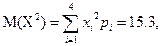
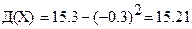
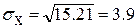
62. В партии 10% нестандартных деталей. Наудачу отобраны четыре детали. Написать биномиальный закон распределения дискретной случайной величины X—числа нестандартных деталей среди четырех отобранных и построить многоугольник полученного распределения.
63. Две игральные кости одновременно бросают два раза. Написать биномиальный закон распределения дискретной случайной величины X—числа выпадений четного числа очков на двух игральных костях.
64. В партии из 10 деталей имеется 8 стандартных. Наудачу отобраны две детали. Обставить закон распределения числа стандартных деталей среди отобранных.
65. Завод отправил на базу 500 изделий. Вероятность повреждения изделия в пути равна 0,002. Найти вероятности того, что в пути будет повреждено изделий: а) ровно три; б) менее трех; в) более трех; г) хотя бы одно.
66. Дискретная случайная величина X принимает три возможных значения: x1 = 4 с вероятностью р1 = 0,5; x2 = 6 с вероятностью p2 = 0,3 и х3 с вероятностью р3. Найти x3 и р3, зная, что М(Х)=8.
67. Дан перечень возможных значений дискретной случайной величины X: x1= 1, x2 = 2, x3 = 3, а также известны математические ожидания этой величины и ее квадрата: M(Х) = 2,3, М(Х2) = 5,9. Найти вероятности, соответствующие возможным значениям X.
68. Случайные величины X и Y независимы. Найти дисперсию случайной величины Z = 3X + 2Y, если известно, что D(X) = 5, D(Y) = 6.
69. Найти дисперсию и среднее квадратическое отклонение дискретной случайной величины X, заданной законом распределения:
а) X 4,3 5,1 10,6. б) X 131 140 160 180.
р 0,2 0,3 0,5 р 0,05 0,10 0,25 0,60
70. Найти дисперсию дискретной случайной величины X—числа появлений события А в двух независимых испытаниях, если вероятности появления события в этих испытаниях одинаковы и известно, что M(Х)=0,9.
71. Дискретная случайная величина X задана законом распределения:
X 1 3
р 0,4 0,6
Найти начальные моменты первого, второго и третьего порядка.
Дата добавления: 2016-03-15; просмотров: 1480;
