Равномерное и показательное

Распределения

Равномерным называют распределение непрерывной случайной величины X, если на интервале (a,b), которому принадлежат все возможные значения X, плотность сохраняет постоянное значение, а вне этого интервала равна нулю, т.е.

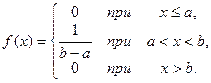
Показательным (экспоненциальным) распределением называют распределение вероятностей непрерывной случайной величины X, которое описывается плотностью

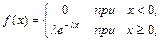
где λ – постоянная положительная величина. Функция распределения показательного закона

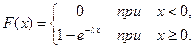
Математическое ожидание и дисперсия соответственно равны

; ;

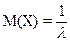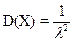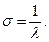
Пример 88. Цена деления шкалы амперметра равна 0,10А. Показания амперметра округляют до ближайшего целого деления. Найти вероятность того, что при отсчете будет сделана ошибка, превышающая 0,02А.

Решение. Ошибку округления можно рассматривать как случайную величину Х, которая распределена равномерно в интервале (0;0,1) между двумя целыми делениями. Следовательно,

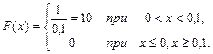
Тогда .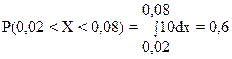

Пример 89. Длительность времени безотказной работы элемента имеет показательное распределение . Найти вероятность того, что за время длительностью t=100 часов: a) элемент откажет; б) элемент не откажет.

Решение. а) По определению 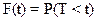, следовательно она определяет вероятность отказа элемента за время t, поэтому

.

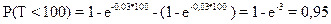б) Событие «элемент не откажет» является противоположным рассмотренному, поэтому его вероятность

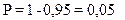
90. Радиоэлектронный блок собирается на поточной линии, такт сборки 2 мин. Готовый блок снимается с конвейера для контроля и регулировки в произвольный момент времени в пределах такта. Найти математическое ожидание и среднее квадратическое отклонение времени нахождения готового блока на конвейере. Время нахождения блока на конвейере подчиняется зако­ну равномерного распределения случайных величин.

91. Вероятность выхода из строя РЭА за определенное время выражается формулой 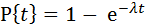. Определить среднее время работы РЭА до выхода из строя.

92. Разрабатываемый спутник связи должен характеризоваться средним временем наработки на отказ 5 лет. Считая реальное время наработки на отказ случайной экспоненциально распределенной величиной, определите вероятность того, что

а) спутник проработает менее 5 лет,

б) спутник проработает не менее 10 лет,

в) спутник откажет в течение 6-го года.

93. Некий квартиросъемщик купил четыре лампочки накаливания со средним сроком службы 1000 ч. Одну из них он установил в настольную лампу, а остальные оставил про запас, на случай, если лампа перегорит. Определите:

а) ожидаемую суммарную продолжительность службы четырех ламп,

б) вероятность того, что четыре лампы в сумме проработают 5000 часов или более,

в) вероятность того, что общий срок службы всех ламп не превысит 2000 часов.

94. Цена деления шкалы измерительного прибора равна 0,2. Показания прибора округляют до ближайшего целого деления. Найти вероятность того, что при отсчете будет сделана ошибка: а) меньшая 0,04; б) большая 0,05.

95. Автобусы некоторого маршрута идут строго по расписанию. Интервал движения 5 мин. Найти вероятность того, что пассажир, подошедший к остановке, будет ожидать очередной автобус менее 3 мин.

96. Найти математическое ожидание случайной величины X, распределенной равномерно в интервале (2, 8).

97. Найти дисперсию и среднее квадратическое отклонение случайной величины X, распределенной равномерно в интервале (2, 8).

98. Испытывают два независимо работающих элемента. Длительность времени безотказной работы первого элемента имеет показательное распределение 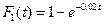, второго 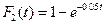. Найти вероятность того, что за время длительностью t=6 ч: а) оба элемента откажут; б) оба элемента не откажут; в) только один элемент откажет; г) хотя бы один элемент откажет.