Неравномерное движение по окружности
 Математическая справка: составляющие векторы.Пусть имеется некоторый вектор
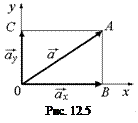
Математическая справка: составляющие векторы.Пусть имеется некоторый вектор 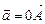 . Проведем через его начало – точку 0, координатные оси 0х и 0у (рис. 12.5). А из конца вектора – точки А опустим перпендикуляры АВ и АС на оси 0х и 0у. Тогда векторы
. Проведем через его начало – точку 0, координатные оси 0х и 0у (рис. 12.5). А из конца вектора – точки А опустим перпендикуляры АВ и АС на оси 0х и 0у. Тогда векторы 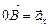 и
и 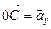 называются составляющими вектора
называются составляющими вектора  по осям 0х и 0у. При этом
по осям 0х и 0у. При этом  =
= 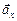 +
+ 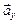 .
.
Заметим, что 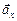 и
и 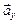 – это не проекции вектора
– это не проекции вектора  на оси 0х и 0у, так как проекция вектора – скалярная величина. Составляющие вектора
на оси 0х и 0у, так как проекция вектора – скалярная величина. Составляющие вектора  – это векторы!
– это векторы!
 Зная составляющие
Зная составляющие 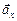 и
и 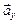 , легко найти модуль вектора
, легко найти модуль вектора  : |
: |  |=
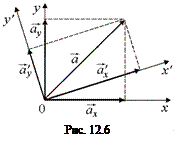
|= 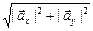 . Заметим также, что один и тот же вектор можно разложить на разные составляющие (рис. 12.6): в системе координат х0у
. Заметим также, что один и тот же вектор можно разложить на разные составляющие (рис. 12.6): в системе координат х0у  =
= 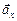 +
+ 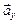 , в системе отсчета х¢0у¢
, в системе отсчета х¢0у¢  =
= 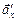 +
+ 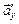 .
.
Нормальное, тангенциальное
И полное ускорения
Пусть тело движется по некоторой кривой L и в определенный момент времени t оно находится в некоторой точке 0, и его ускорение равно  (рис. 12.7). Проведем через точку 0 касательную к траектории. Введем две координатные оси: t, направленную по касательной к траектории, и
(рис. 12.7). Проведем через точку 0 касательную к траектории. Введем две координатные оси: t, направленную по касательной к траектории, и 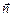 , перпендикулярную к касательной. Тогда вектор
, перпендикулярную к касательной. Тогда вектор  можно представить в виде:
можно представить в виде:  =
= 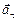 +
+ 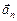 , где
, где 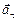 и
и 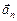 – составляющие вектора
– составляющие вектора  по осям
по осям 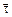 и
и 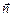 . Вектор
. Вектор 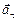 называется касательным или тангенциальным (от слова "тау" – t) ускорением, вектор
называется касательным или тангенциальным (от слова "тау" – t) ускорением, вектор 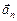 , называется нормальным ускорением.
, называется нормальным ускорением.
Рис. 12.7 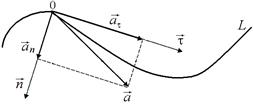
Читатель: Простите за глупый вопрос, но почему ускорение называется нормальным? Имеется в виду, что оно психически здоровое, т.е. не сумасшедшее?
Автор: Нет, просто в курсе аналитической геометрии вместо слова "перпендикуляр" часто употребляют слово "нормаль". Нормальное ускорение – значит, перпендикулярное к касательной.
Читатель: И еще у меня сомнение: получается, что у одного и того же тела в один и тот же момент времени... сразу три ускорения:  ,
, 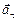 и
и 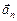 ?
?
Автор: Нет, конечно. Ускорение одно –  , а
, а 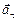 и
и 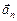 – ускорения только по названию. На самом деле это всего лишь составляющие вектора
– ускорения только по названию. На самом деле это всего лишь составляющие вектора  по осям
по осям 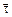 и
и 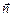 . Этих составляющих может быть сколько угодно, если вместо осей
. Этих составляющих может быть сколько угодно, если вместо осей 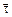 и
и 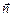 взять какие-нибудь другие оси. Просто разложение вектора ускорения
взять какие-нибудь другие оси. Просто разложение вектора ускорения  именно по этим осям, как мы убедимся, наиболее удобно. Заметим, что если
именно по этим осям, как мы убедимся, наиболее удобно. Заметим, что если 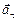 и
и 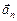 известны, то
известны, то  , которое еще называют полным ускорением по модулю равно |
, которое еще называют полным ускорением по модулю равно |  | =
| = 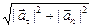 .
.
Замечание. В каждой точке криволинейной траектории направления осей 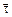 и
и 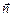 , вообще говоря, разные. Поэтому эти оси называют мгновенными осями, их направление определено только в данное мгновение.
, вообще говоря, разные. Поэтому эти оси называют мгновенными осями, их направление определено только в данное мгновение.
 Задача 12.1. Найти полное, нормальное и тангенциальное ускорения для следующих случаев: 1) тело свободно падает с ускорением
Задача 12.1. Найти полное, нормальное и тангенциальное ускорения для следующих случаев: 1) тело свободно падает с ускорением 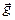 , 2) тело равномерно движется по окружности радиуса R со скоростью υ.
, 2) тело равномерно движется по окружности радиуса R со скоростью υ.
Решение. В первом случае траектория – прямая. Ось 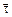 совпадает по направлению с вектором
совпадает по направлению с вектором 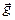 ,
, 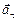 =
= 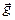 ,
, 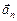 = 0,
= 0,  =
= 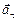 +
+ 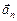
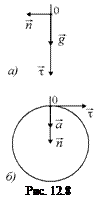
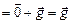 (рис. 12.8,а). Во втором случае полное ускорение направлено к центру окружности, причем
(рис. 12.8,а). Во втором случае полное ускорение направлено к центру окружности, причем 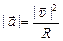 . Значит,
. Значит, 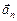 =
=  ,
, 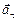 = 0 (рис. 12.8,б).
= 0 (рис. 12.8,б).
СТОП! Решите самостоятельно: А2–А4.
Задача 12.2.Тело движется по окружности радиусом R равноускоренно с путевым ускорением a без начальной скорости. Найти нормальное, тангенциальное и полное ускорения в произвольный момент времени t, если в начальный момент времени тело покоилось.
| R, t, a | Решение. Пусть в момент времени t тело находилось в точке М и имело скорость  , а через малое время Dt ® 0 тело находилось в точке М' и имело скорость , а через малое время Dt ® 0 тело находилось в точке М' и имело скорость 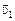 . .
|
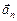 = ? = ? 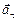 = ? = ?
 = ? = ?
| |
Для того чтобы найти приращение скорости  за это время, нужно из вектора
за это время, нужно из вектора 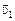 вычесть вектор
вычесть вектор  или, что то же самое, прибавить вектор (–
или, что то же самое, прибавить вектор (–  ):
):
ПРИРАЩЕНИЕ = (ТО ЧТО СТАЛО) – (ТО ЧТО БЫЛО)
или
 =
= 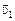 –
–  =
= 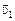 + (–
+ (–  ).
).
Как видно из рис. 12.9, |  | = М1В, |
| = М1В, | 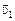 | = М1А. Введем ось
| = М1А. Введем ось 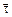 , направленную по касательной к окружности в точке М1 и ось
, направленную по касательной к окружности в точке М1 и ось 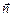 , перпендикулярную оси
, перпендикулярную оси 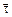 и направленную по радиусу М1О к центру окружности. Разложим вектор
и направленную по радиусу М1О к центру окружности. Разложим вектор  на составляющие по осям
на составляющие по осям 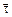 и
и 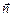 . Для этого опустим перпендикуляр из конца вектора
. Для этого опустим перпендикуляр из конца вектора  – точки В на
– точки В на 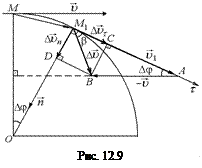 оси
оси 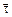 и
и 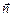 : ВС ^
: ВС ^ 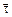 и ВD ^
и ВD ^ 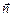 . Тогда
. Тогда 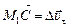 и
и  – составляющие вектора
– составляющие вектора  по осям
по осям 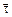 и
и 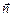 . При этом
. При этом
 =
= 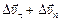 .
.
Полное ускорение равно
 .
.
Поскольку вектор 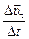 направлен вдоль оси
направлен вдоль оси 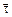 , а вектор
, а вектор  направлен вдоль оси
направлен вдоль оси 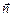 , то эти векторы представляют coбой составляющие полного ускорения
, то эти векторы представляют coбой составляющие полного ускорения  по осям
по осям 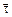 и
и 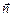 , т.е. нормальное и тангенциальное ускорения:
, т.е. нормальное и тангенциальное ускорения: 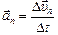 ,
, 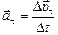 .
.
Найдем абсолютные значения нормального и тангенциального ускорений.
Нормальное ускорение.Рассмотрим треугольники MОM1 и АВС. В них ÐМОМ1 = ÐСАВ как углы со взаимно перпендикулярными сторонами (ОМ^АВ и ОМ1^АС, так как радиус, проведенный в точку касания перпендикулярен касательной). Поскольку время Dt мало, ÐDj = ÐСАВ ® 0; ÐВСА = 90° по построению, следовательно, и ÐABC ® 90°. Тогда можно считать, что АВ @ АС, т.е DАВС – равнобедренный. С учетом этого приближения DАВС подобен DМОМ' как равнобедренные с равными углами при вершинах. Отсюда
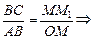
 ,
,
где 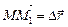 – перемещение тела. Поскольку угол ÐМОМ¢ мал, отрезок ММ1 практически совпадает с дугой окружности
– перемещение тела. Поскольку угол ÐМОМ¢ мал, отрезок ММ1 практически совпадает с дугой окружности 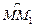 и модуль перемещения |
и модуль перемещения | 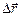 | практически равен пройденному пути –длине дуги
| практически равен пройденному пути –длине дуги 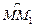 . Следовательно, |
. Следовательно, | 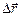 | = υDt. Отсюда
| = υDt. Отсюда
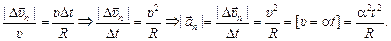
Итак:
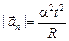 .
.
Тангенциальное ускорение. Найдем модуль вектора 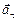 :
:
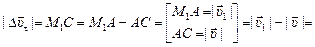
= 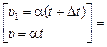 a(t + Dt) –at = aDt,
a(t + Dt) –at = aDt,
т.е. величина  равна изменению модуля вектора скорости за время Dt. Модуль тангенциального ускорения равен:
равна изменению модуля вектора скорости за время Dt. Модуль тангенциального ускорения равен:
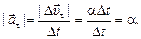
Полное ускорение.Мы определили, что
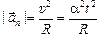 ,
, 
Модуль полного ускорения равен
|  | =
| = 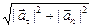 =
=  .
.
Направление вектора  задается углом b = ÐВМ1С, который вектор полного ускорения составляет с осью
задается углом b = ÐВМ1С, который вектор полного ускорения составляет с осью 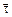 (
( 
 ).
).
В DСМ1В М1С = 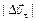 , ВС =
, ВС = 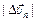 ,
,
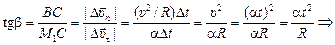
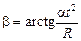 .
.
Читатель: Так какой же физический смысл имеют составляющие полного ускорения 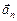 и
и 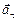 ?
?
Автор: Заметим, что модуль тангенциального ускорения 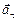 , как мы выяснили в задаче 12.2, равен отношению приращения модуля скорости ко времени, в течение которого это приращение произошло:
, как мы выяснили в задаче 12.2, равен отношению приращения модуля скорости ко времени, в течение которого это приращение произошло:  , т.е. тангенциальное ускорение характеризует быстроту изменения модуля скорости.
, т.е. тангенциальное ускорение характеризует быстроту изменения модуля скорости.
Нормальное ускорение по модулю равно 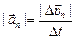 , т.е.
, т.е. 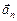 характеризует скорость изменения нормальной составляющей скорости. Чем больше |
характеризует скорость изменения нормальной составляющей скорости. Чем больше | 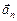 |, тем быстрее тело меняет направление движения.
|, тем быстрее тело меняет направление движения.
Ответ: 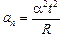 ; аt = a;
; аt = a; 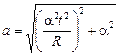 , вектор
, вектор  составляет с касательной угол
составляет с касательной угол 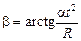 .
.
СТОП! Решите самостоятельно: А5, В1, В2, В5, С2.
Кривизна кривой
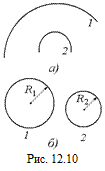 Автор: Как Вы думаете, какая кривая на рис. 12.10,а "кривее": 1 или 2?
Автор: Как Вы думаете, какая кривая на рис. 12.10,а "кривее": 1 или 2?
Читатель: Признаться, Ваш вопрос не совсем ясен, но чисто интуитивно, по-моему, кривая 2 "кривее", чем кривая 1. Но я с трудом понимаю, как можно измерять такое туманное понятие, как кривизна.
Автор: А как Вы думаете, какая окружность на рис. 12.10,б "кривее": 1 или 2?
Читатель: "Кривее", конечно, маленькая, т.е. вторая, так как R2 < R1.
Автор: Верно! Вот Вы, кстати, сами того не заметив, и указали единицу кривизны  окружности – ее радиус. Чем меньше радиус, тем "кривее" окружность, чем больше радиус, тем она "прямее". Оно и по житейски понятно: когда едешь, например, по московской кольцевой автодороге (радиус » 20 км) – полная иллюзия, что едешь по прямой. Ну, а если автомобиль поворачивает за угол – уж тут никаких сомнений – едешь по кривой. При R ® ¥ окружность вообще превращается в прямую.
окружности – ее радиус. Чем меньше радиус, тем "кривее" окружность, чем больше радиус, тем она "прямее". Оно и по житейски понятно: когда едешь, например, по московской кольцевой автодороге (радиус » 20 км) – полная иллюзия, что едешь по прямой. Ну, а если автомобиль поворачивает за угол – уж тут никаких сомнений – едешь по кривой. При R ® ¥ окружность вообще превращается в прямую.
Читатель: Да, с окружностями понятно. Но как быть с неокружностями?
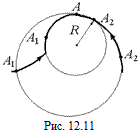 Автор: Как известно, через любые три точки, не лежащие на одной прямой, можно провести окружность. Пусть у нас имеется некоторая кривая и нас интересует ее кривизна в некоторой точке А. Возьмем слева и справа от точки А точки A1 и А2 и проведем через эти три точки окружность (рис. 12.11). Затем немного сблизим точки А1 и А2 с точкой А и проведем через них еще одну окружность. Будем продолжать этот процесс, постепенно уменьшая расстояния между точками. Когда точки А1, А и А2 будут находиться достаточно близко друг к другу, проведенная через них окружность практически будет совпадать с нашей кривой на некотором малом участке дуги кривой около точки А. Радиус этой окружности и характеризует кривизну кривой в данной точке и называется радиусом кривизны.
Автор: Как известно, через любые три точки, не лежащие на одной прямой, можно провести окружность. Пусть у нас имеется некоторая кривая и нас интересует ее кривизна в некоторой точке А. Возьмем слева и справа от точки А точки A1 и А2 и проведем через эти три точки окружность (рис. 12.11). Затем немного сблизим точки А1 и А2 с точкой А и проведем через них еще одну окружность. Будем продолжать этот процесс, постепенно уменьшая расстояния между точками. Когда точки А1, А и А2 будут находиться достаточно близко друг к другу, проведенная через них окружность практически будет совпадать с нашей кривой на некотором малом участке дуги кривой около точки А. Радиус этой окружности и характеризует кривизну кривой в данной точке и называется радиусом кривизны.
Задача 12.3. Тело брошено под углом a к горизонту с начальной скоростью υ0. Определить радиус кривизны траектории: 1) в верхней точке полета; 2) в момент начала движения. Ускорение свободного падения равно 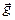 .
.
Решение. Отметим, что в обоих случаях полное ускорение равно 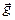 и направлено вертикально вниз.
и направлено вертикально вниз.
1. В верхней точке полета скорость равна (рис. 12.12,а) υв = =υ0cosa, тогда 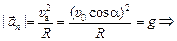
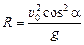 .
.
а)  б)
б) 
Рис. 12.12
Заметим, что при a ® 90° (это соответствует случаю тела, брошенного вертикально вверх) R ® 0. В верхней точке полета радиус кривизны траектории тела, брошенного вертикально вверх действительно очень мал (рис. 12.12,б).
В точке 0, в начальный момент полета, нормальное ускорение равно  . С другой стороны,
. С другой стороны,
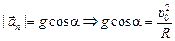 Þ
Þ 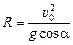 .
.
Заметим, что при a ® 90° cosa ® 0, R ® ¥, т.е. при a ® 90° траектория почти прямолинейная. Действительно, если тело бросить вертикально вверх, т.е. под углом 90° к горизонту, то оно будет в начальный момент двигаться по прямой (см. рис. 12.12,б).
СТОП! Решите самостоятельно: В6, В7, С4.
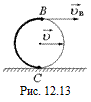 Задача 12.4. Колесо катится без проскальзывания с постоянной скоростью υ. Определить мгновенные скорости точек В и С относительно центра колеса и относительно земли (рис. 12.13).
Задача 12.4. Колесо катится без проскальзывания с постоянной скоростью υ. Определить мгновенные скорости точек В и С относительно центра колеса и относительно земли (рис. 12.13).
Решение. Сначала выясним, что значит "без проскальзывания"? Это значит, что точка С, которая касается поверхности земли, неподвижна относительно земли в момент касания.
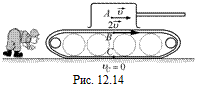 Чтобы лучше понять сказанное, пронаблюдайте как-нибудь на досуге за движущимся танком (бульдозером, трактором, БТР), словом, за любым механизмом на гусеничном ходу. Вы увидите, что все точки, находящиеся на нижней части гусеницы, например точка С (рис. 12.14), неподвижны относительно земли: гусеница намертво сцепляется с грунтом. Сам же танк движется при этом вперед с некоторой скоростью υ. Ясно, что с такой же скоростью движутся вперед все неподвижные точки танка, точка А, например.
Чтобы лучше понять сказанное, пронаблюдайте как-нибудь на досуге за движущимся танком (бульдозером, трактором, БТР), словом, за любым механизмом на гусеничном ходу. Вы увидите, что все точки, находящиеся на нижней части гусеницы, например точка С (рис. 12.14), неподвижны относительно земли: гусеница намертво сцепляется с грунтом. Сам же танк движется при этом вперед с некоторой скоростью υ. Ясно, что с такой же скоростью движутся вперед все неподвижные точки танка, точка А, например.
Что же касается верхней части гусеницы, то она движется вперед со скоростью 2υ (точка В), т.е. вдвое большей скорости танка.
Читатель: А почему именно ВДВОЕ большей?
Автор: Давайте разберемся с этим вопросом так, чтобы не осталось никаких сомнений.
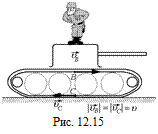
 Если считать, что нижняя часть гусеницы неподвижна относительно земли, а сам танк едет вперед со скоростью υ, то ясно, что относительно танка нижняя часть гусеницы движется назад с такой же скоростью υ (рис. 12.15).
Если считать, что нижняя часть гусеницы неподвижна относительно земли, а сам танк едет вперед со скоростью υ, то ясно, что относительно танка нижняя часть гусеницы движется назад с такой же скоростью υ (рис. 12.15).
Считая гусеницу нерастяжимой, мы должны заключить, что все точки гусеницы должны иметь одинаковую по модулю мгновенную скорость υ относительно танка. А раз так, то и точка В, расположенная на верхней части гусеницы, движется относительно танка со скоростью υ. Причем движется вперед. А поскольку сам танк тоже движется вперед со скоростью υ относительно земли, то скорость точки В относительно земли равна υ + υ = 2υ.
Колесо отличается от гусеницы только тем, что касается земли лишь в одной точке – точке С (рис. 12.15). Реальное колесо, конечно, касается земли определенной частью своей поверхности, поэтому приведенные выше рассуждения про гусеницу танка в полной мере справедливы и для колеса. Отсюда υс = 0, υв = 2υ относительно земли; υс = υв = υ относительно центра колеса.
СТОП! Решите самостоятельно: А6, В8, С5.
Дата добавления: 2016-04-11; просмотров: 3765;
