Задачи средней трудности. В1. При равноускоренном движении тела по окружно­сти полное ускорение а и линейная скорость υ тела образуют угол a = 30°

В1. При равноускоренном движении тела по окружно­сти полное ускорение а и линейная скорость υ тела образуют угол a = 30°. Найти отношение центростремительного и касательного ускорений.

В2. Материальная точка движет­ся по окружности радиуса R = 20 см равноускоренно с касательным уско­рением а_t= 5,0 см/с². Через какое время t после начала движения центростремительное ускорение а_п будет боль­ше а_t в п = 2 раза?

В3. Материальная точка, двигаясь равноускоренно по окружности радиуса R = 1,0 м, прошла за время t₁ = 10 с путь s = 50 м. С каким центростремительным ускорением а_п дви­галась точка спустя время t₂ = 5,0 c после начала движения?

В4. Тело брошено горизонтально с начальной скоростью υ₀ = 15 м/с. Найти нормальное а_п и касательное а_t ускоре­ния через время t = 10 с после начала движения тела.

В5. Тело бросили под углом к горизонту (рис. 12.28).

1. В какой из точек – А или В – полное ускорение тела больше?

2. В какой из этих точек больше касательное ускорение а_t?

3. Каков смысл касательного ускорения а_t?

4. В какой из этих точек нормальная (перпендикулярная к вектору скорости) составляющая а_п полного ускорения больше?

5. Каков физический смысл ускорения а_п?

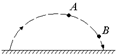
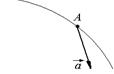
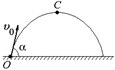
Рис. 12.28 Рис. 12.29 Рис. 12.30

В6. Точка движется по криволинейной траектории (рис. 12.29). В некоторой точке А этой траектории вектор полного ускорения составляет угол a = 30° с вектором скорости и равен по модулю 20 м/с².

1. Чему равно касательное ускорение а_t в этой точке?

2. Чему равен радиус кривизны R траектории в этой точке, если υ_А = = 5 м/с².

В7. Тело брошено из точки О под углом a к горизонту с начальной скоростью υ₀, где a = 60° и υ₀ = 20 м/с (рис. 12.30). Во сколько раз радиус кривизны траектории в точке О больше радиуса кривизны в точке С (вершине параболы)?

В8. Почему, когда колесо катится, то часто бывает, что нижние спицы видны отчетливо, а верхние спицы как будто сливаются?

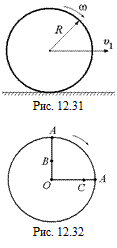
В9. На шероховатую горизонтальную плоскость бросают обруч радиусом R с линейной скоростью υ₁. Одновременно ему сообщается вращательное движение в таком направлении, что он должен катиться по плоскости в ту же сторону (рис. 12.31). При какой угловой скорости w обруч покатится по плоскости без скольжения?

В10. Автомобиль движется прямолинейно с постоянной скоростью υ = 20 м/с. Каково ускорение верхней точки его колеса? Радиус колеса равен R = 0,25 м.

В11. На диске проигрывателя из его центра мелом проведена линия ОА (рис. 12.32). Муха ползет строго по этой линии со скоростью υ_м = 0,50 см/с, а сам диск вращается с угловой скоростью w = 0,10 рад/с. Чему равна скорость мухи относительно земли (модуль и направление) в тот момент, когда она находится: 1) в точке В, если ОВ = = R₁ = 2,0 см; 2) в точке А, если ОА = R₂ = 10 см? Является ли в этом случае переносная скорость постоянной величиной?

В12. Вагон А движется по закруглению радиусом R с линейной скоростью υ, вагон В – прямолинейно со скоростью w (рис. 12.33). Рас­стояние ОВ равно l. Найти скорость и вагона В относительно вагона А в момент, когда расстояние АВ минимально и точка А лежит на прямой ОВ.

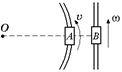Рис. 12.33 Рис. 12.34

В13. Какое расстоянии пройдет человек, прежде чем он дойдет до цилиндра (рис. 12.34). Доска движется по цилиндру без проскальзывания.

В14.Ось вращающегося диска движется поступательно в горизонтальном направлении со скоростью υ. Ось гори­зонтальна, направление ее движения перпендикулярно к ней самой. Найти мгновенную скорость υ верхней точки диска, если мгновенная скорость нижней точки диска равна υ₂.

В15.Зубчатое колесо диаметром D₁ находится во внутреннем зацеплении с зубчатым колесом диаметром D₂, расположенным внутри первого колеса (рис. 12.35). Колесо D₁ делает п₁ об/с, вращаясь вокруг неподвижной оси. Найти диаметр колеса D₂, если оно должно делать п₂ об/с.

Рис. 12.35 Рис. 12.36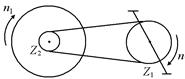

В16.Диаметр колеса велосипеда «Пенза» d = 70 см, ведущая зубчатка имеет z₁ = 48 зубцов, а ведомая z₂ = 18 зубцов (рис. 12.36). С какой скоростью движется велосипедист на этом велосипеде при частоте вращения педалей п = 1,0 об/с? С какой скоростью движется велосипедист на складном велосипеде «Кама» при той же частоте вращения педалей, если у этого велосипедиста соответственно d = 50 см, Z₂ = 15 зубцов?

В17.Катушка, состоящая из цилиндрической части и двух одинаковых сплошных дисков, катится своей цилиндрической частью без скольжения по шеро­ховатому бруску, расположен­ному горизонтально, с постоян­ной скоростью υ (рис. 12.37). Ради­ус цилиндрической части г, дисков R. Какую скорость име­ют точки А и В, находящиеся на ободе одного из дисков?

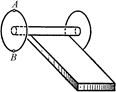
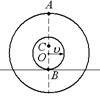
Рис. 12.37 Рис. 12.38 Рис. 12.39

В18. Какие точки дисков из предыдущей задачи имеют мгновенную скорость, равную по величине скорости оси катушки?

В19. Начертить траектории точек А, В и С катушки (рис. 12.38), которая катится по бруску без скольжения своей цилиндрической частью.

В20. Вагон движется по рельсам со скоростью υ. Найти линейную скорость точек т, п, р, q обода и реборды колеса (рис. 12.39). Диаметры колеса и реборды равны d и D соответственно. Задачу решить для неподвижного наблюдателя, находящегося вне вагона, и для наблюда­теля, движущегося с вагоном.

Задачи трудные

С1. Тело движется по окружности радиуса R, при этом зависимость танген­циального ускорения тела от времени имеет вид, представленный на ри­с. 12.40. Нарисуйте график зави­симости нормального ускорения от времени, если начальная скорость тела равна нулю.

С2. Поезд въезжает на закругленный участок пути с на­чальной скоростью υ₀ = 54 км/ч и проходит равноускоренно расстояние s = 600 м за время t = 30 с. Радиус закругления R = 1,0 км. Найти скорость υ и полное ускорение а поезда в конце этого участка пути.

С3. Автомобиль начал движение по выпуклому мосту со скоростью, изменяющейся по закону υ = . Каково ускорение автомобиля в тот момент, когда он опишет дугу в a радиан?

С4. Тело бросили горизонтально с большой высоты, придав ему начальную скорость υ₀ = 10 м/с. Каков радиус кривизны траектории в той точке, где оказалось тело, пролетев по горизонтали расстояние l = 10 м? Чему равно касательное ускорение в этой точке?

С5.Велосипедист едет с постоянной скоростью υ по прямолинейному участку дороги. Найти мгновенные линейные скорости точек А, В, С, D, E, лежащих на ободе колеса (рис. 12.41), относительно земли.

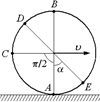Рис. 12.41 Рис. 12.42

С6. По горизонтальной поверхности катится без проскальзывания колесо (рис. 12.42). Скорость поступательного движения колеса равна υ. Укажите точки на колесе, скорости которых относительно поверхности также равны υ.

С7. Гусеница трактора состоит из п звеньев. Длина каждого звена а. Радиусы колес, на которые надета гусеница, R. Трактор движется со скоростью υ. Предполагается, что гусеница не провисает.

1.Какое число звеньев гусеницы движется в данный мо­мент поступательно? Какое число звеньев покоится (относительно земли) и какое число звеньев участвует во вращательном движении?

2. Трактор прошел путь s >> na. Сколько времени каждое звено гусеницы двигалось поступательно, покоилось и участвовало во вращательном движении?

C8.Кольцо радиусом R катится без скольжения по горизонталь­ной поверхности с угловой скоростью w (рис. 12.43). Найти зависимость координат точки А кольца от времени. Начальные условия: х_А = 0; у_а = 0; j = 0.

Рис. 12.43 Рис. 12.44

С9. Круглая горизонтальная платформа вращается вокруг своей оси со скоростью w = 3,0 с^–1 (рис. 12.44). Шар А катится в направ­лении АО со скоростью 7,0 м/с. Расстояние АО равно 8,0 м (в данный момент). Найти скорость шара относительно платформы.

С10. Над экватором планеты движется спутник в сторону ее вращения. Скорость спутника υ₁ = 6 км/с, а скорость точек экватора υ₂ = 1 км/с. Найти скорость спутника относительно планеты, зная, что радиус планеты равен R₁ = 1000 км, а радиус орбиты спутника равен R₂ = 2000 км.

С11. На киноэкране демонстрируется движущаяся повозка. Радиус колес R = 0,40 м, каждое колесо имеет N = 6 спиц. Съемка производилась со скоростью 24 кадра в секунду. При какой минимальной скорости движения повозки колеса на экране будут казаться: а) вращающимися «не в ту» сторону; б) неподвижными относительно повозки?

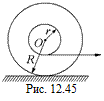С12. Катушка с намотанной на ней нитью лежит на горизонтальном столе и может катиться по нему без скольжения. Внутренний радиус катушки равен r, внешний R (рис. 12.45). С какой скоростью и будет перемещаться ось катушки, если конец нити тянуть в горизон­тальном направлении со скоростью υ?

С13.Катушка с намотанной на ней нитью катится без скольжения по горизонтальной плоскости благодаря вытягиванию нити в горизон­тальном направлении со скоростью υ. Радиусы внутренней и внешней поверхностей катушки соответственно равны r и R. Найти скорость точек О и А (рис. 12.46).

С14. Кривошип ОА, вращаясь вокруг оси О, приводит в движение колесо 1 радиуса R = 20 см, катящееся по внутренней поверхности неподвижного круга 2 (рис. 12.47). Колесо 1, соприкасаясь с колесом 3 радиуса r = 10 см, заставляет его вращаться вокруг оси О. (Ко­лесо 3 свободно надето на ось О и не связано с кривошипом ОА.) Во сколько раз угловая скорость колеса 3 больше угловой скорости кривошипа ОА?

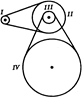
Рис. 12.46 Рис. 12.47 Рис. 12.48

С15. Движение от шкива I (рис. 12.48) к шкиву IV передается при помощи двух ременных передач. Найти частоту вращения (в об/мин) шкива IV, если шкив I делает 1200 об/мин, а радиусы шкивов r₁ = 8,0 см, r₂ = 32 см, r₃ = 11 см, r₄ = 55 см. Шкивы II и III жестко укреплены на одном валу.

С16. Шарикоподшипник состоит из двух колец – внутреннего радиуса R₂ и внешнего радиуса R₁ – и расположенных между ними шариков, радиус которых r. Внешнее кольцо вращается с линейной скоростью υ₁, а внутреннее – со скоростью υ₂. Найти линейную скорость υ и скорость вращения w шариков вокруг собственного центра в предположении, что проскальзывание между шариками и кольцами отсутствует (рис. 12.49).

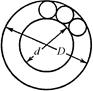
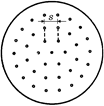
Рис. 12.49 Рис. 12.50 Рис. 12.51

С17. Шарикоподшипник поддерживает конец оси вала, вращающегося с угловой скоростью w. Диаметр оси вала d (рис. 12.50), диаметр обоймы шарикоподшипника D. Найти линейную скорость движения центра одного из шариков, если обойма неподвижна и если обойма вращается с угловой ско­ростью W. Считать, что в обоих случаях шарики катятся по валу и обойме без скольжения.

С18.Диск с отверстиями, про­сверленными по окружностям на расстоянии s = 1,0 см друг от друга (рис. 12.51), освещен сзади лампой. Диск вращается с частотой п = 30 об/мин. На каком расстоянии r от центра диска мы увидим сплошной светящийся круг? (Чело­веческий глаз не ощущает колебаний яркости, если они происходят чаще, чем 16 раз в секунду.)

С19.Два автомобиля движутся друг за другом по дороге с одинаковой скоростью υ = 72 км/ч. При каком минимальном расстоянии l между ними камешек, застрявший между сдвоенными шинами переднего грузового автомобиля, не может попасть на задний автомобиль?