Мгновенный центр вращения

На рис. 12.15 точка С колеса, которая соприкасается с землей, неподвижна относительно земли в данный момент. Поэтому ее можно рассматривать как некоторый центр, относительно которого поворачивается все колесо. При этом скорость центра колеса равна υ.

Задача 12.5. Определить мгновенные скорости точек С и D (рис. 12.16), если колесо катится без проскальзывания со скоростью υ, угол a задан.

υ, a	Решение. Относительно мгновенного центра О¢ все точки колеса движутся с одинаковой угловой скоростью w, причем 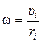, где υi – скорость точки i
υС = ? υD = ?
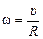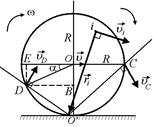относительно земли, а ri – расстояние от данной точки до точки О¢ (см. рис. 12.16). Для точки С: rC = О¢С; для точки D: rD = = О¢D. Найдем w. Поскольку точка О движется со скоростью υ, а ОО¢ = R – радиус колеса, то . Из DОО¢С по теореме Пифагора	Рис. 12.16

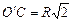, тогда , υ_С = 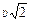. Радиус О¢D точки D найдем из DDО¢В: DB = Rcosa, O¢B = R–Rsina. По теореме Пифагора

.

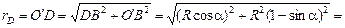
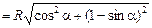Тогда ,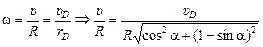

.

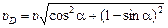Заметим, что вектор скорости перпендикулярен к мгновенному радиусу, так как скорость направлена по касательной к траектории.

Ответ: υ_С = ; .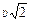

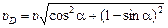СТОП! Решите самостоятельно: С6, С12, С13.