Задачи очень трудные

D1.На экране демонстрируется движущаяся повоз­ка. Радиусы передних колес повозки r = 0,35 м, задних – R = 1,5r. Передние колеса имеют N₁= 6 спиц. Съемочная камера перемещает пленку со скоростью 24 кадра в секунду. Считая, что колеса повозки катятся без скольжения, опреде­лить, с какой минимальной скоростью должна двигаться повозка, чтобы передние колеса ее казались на экране невращающимися? Какое наименьшее число спиц N₂ должны иметь при этом задние колеса, чтобы они также казались невращающимися?

D2. При каких скоростях движения повозки, движущейся слева направо (см. условие задачи D1), кинозрителям бу­дет казаться, что: 1) спицы колес вращаются против часовой стрелки; 2) спицы передних колес и задних колес вра­щаются в противоположные стороны? Число спиц передних и зад­них колес одинаково и равно 6.

D3. Для спуска груза М, привязанного к концу троса (рис. 12.52), намотанного на барабан III, вытягивают со скоростью υ канат А, намотанный на барабан 1. На одной оси с барабаном 1 радиуса r₁ насажено зубчатое колесо I радиуса R₁ жестко скрепленное с ним. Зубчатое колесо I сцеплено с зубчатым колесом 2 радиуса r₂, кото­рое вращается как одно целое с зубчатым колесом II радиуса R₂. Последнее сцеплено с зубчатым колесом 3 радиуса r₃, вращающимся как одно целое с барабаном III радиуса R₃. Определить скорость опускания груза М, если оси всех колес неподвижны.

Рис. 12.52

D4. Стержень, одним концом шарнирно закрепленный на горизон­тальной плоскости, лежит на цилиндре (рис. 12.53). Угловая скорость стержня w. Проскальзывания между цилиндром и плоско­стью нет. Найдите зависимость угловой ско­рости цилиндра от угла a между стрежнем и плоскостью.

D5. Бревно, упираясь нижним своим концом в угол между стеной и землей, касается дна грузовика на высоте Н от земли (рис. 12.54). Найдите угловую скорость бревна в зависимости от угла a между ним и горизонталью, если грузовик отъезжает от стены со скоростью υ.

D6. Цилиндр с намотанной на него нитью, второй конец которой закреплен, находится на горизонтальной подставке, движущейся поступательно с постоянной гори­зонтально направленной скоростью υ. Найти скорость оси цилиндра в зависимости от угла a, образуемого нитью с вертикалью. Относительно подставки цилиндр не про­скальзывает (рис. 12.55).

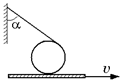Рис.12.55 Рис. 12.56

D7. Конец нити, намотанной на катушку, перекинут через гвоздь, вбитый в стену. Нитку тянут с постоянной скоростью υ. С какой скоростью будет двигаться центр катушки в тот момент, когда нить составляет угол a с вертикалью? Внешний радиус катушки R, внутренний — r. Катушка катится без проскальзывания (рис. 12.56).

D8. С колеса автомобиля, движущегося с постоянной скоростью υ, слетают комки грязи. Радиус колеса равен R. На какую высоту h над дорогой будет отбрасываться грязь, оторвавшаяся от точки А колеса, указан­ной на рис. 12.57? Изменится ли высота h, если колесо будет катиться с пробуксов­кой?

D9.С какой скоростью υ должен ехать автомобиль, чтобы сорвав­шийся с его колеса в точке А (рис. 12.58) застрявший в шине камешек попал в ту же точку колеса, от которой оторвался? Радиус колеса R = 20 см.

Рис. 12.57 Рис. 12.58

D10. При взрыве покоящейся цилиндрической бомбы радиуса R осколки, разлетающиеся в радиальном направле­нии, за время t удаляются от оси цилиндра на расстояние l₁. На какое расстояние l₂ от оси цилиндра удаляются осколки за то же время t, если в момент взрыва бомба будет вращаться вокруг своей оси с угловой скоростью w? Влиянием силы тяжести пренебречь.

_______