Равномерно движущаяся по окружности?
Читатель: Раз материальная точка движется равномерно, то ускорение, вроде бы, должно равняться нулю, ведь Dυ = 0, а значит,
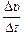 = 0.
= 0.
Автор: Верно. Путевое ускорение материальной точки, равномерно движущейся по окружности действительно равно нулю, так как мгновенная путевая скорость, равная модулю мгновенной скорости перемещения в процессе движения не меняется. Но вектор мгновенной скорости перемещения постоянно меняет направление. Значит, на любом промежутке времени существует и вектор изменения скорости: 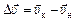 , а следовательно, на любом промежутке времени существует и среднее ускорение
, а следовательно, на любом промежутке времени существует и среднее ускорение 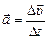 (см. рис. 12.3). Попробуем определить мгновенное ускорение для материальной точки, движущейся по окружности радиуса R с постоянной скоростью υ. Предупреждаю: задача эта – не самая простая.
(см. рис. 12.3). Попробуем определить мгновенное ускорение для материальной точки, движущейся по окружности радиуса R с постоянной скоростью υ. Предупреждаю: задача эта – не самая простая.
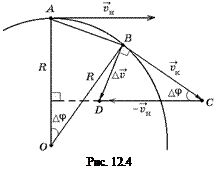 Пусть материальная точка за малый промежуток времени
Пусть материальная точка за малый промежуток времени 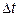 переместилась по дуге окружности из точки А в точку В (рис. 12.4).
переместилась по дуге окружности из точки А в точку В (рис. 12.4).
Напомним, что вектор скорости направлен по касательной к траектории движения (в данном случае к окружности).
Как мы знаем из геометрии, радиус окружности перпендикулярен к касательной к окружности в точке касания. Поэтому радиусы ОА и ОВ перпендикулярны векторам 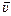 н и
н и 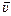 к соответственно: ОА ^
к соответственно: ОА ^ 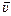 н и OB ^
н и OB ^ 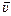 к.
к.
Теперь для того, чтобы построить вектор D 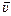 , возьмем вектор (–
, возьмем вектор (– 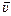 н), поместим начало этого вектора в конец вектора
н), поместим начало этого вектора в конец вектора 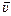 к – точку С и построим вектор D
к – точку С и построим вектор D 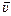 =
= 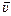 к + (–
к + (– 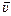 н) =
н) = 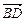 (см. рис. 12.4).
(см. рис. 12.4).
Пусть ÐАОВ, на который повернулся радиус окружности при перемещении материальной точки из А в В, равен Dj, тогда ÐВСD = =ÐАОВ = Dj, как углы со взаимно перпендикулярными сторонами: ОА^СD и OB^ВС.
Теперь рассмотрим два треугольника: АОВ и ВСD. Они равнобедренные и имеют равные углы при вершине: АО = OB = R, ВС = = СD = υ. Следовательно, эти треугольники подобны: DАОВ ∾ DВСD. А из подобия треугольников следует:
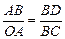 , (1)
, (1)
где ОА = R, ВD = |D 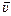 |, ВС = υ.
|, ВС = υ.
Хорда АВ при малом угле Dj практически совпадает с дугой 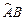 , а дуга
, а дуга 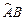 – это путь, пройденный материальной точкой, которая двигалась со скоростью υ в течение времени Dt, следовательно: АВ = υDt. Подставляя значения ОА, ВD, ВС и АВ в (1), получим:
– это путь, пройденный материальной точкой, которая двигалась со скоростью υ в течение времени Dt, следовательно: АВ = υDt. Подставляя значения ОА, ВD, ВС и АВ в (1), получим:
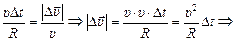
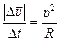 . (2)
. (2)
Но 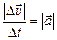 , то есть это модуль искомого мгновенного ускорения, следовательно:
, то есть это модуль искомого мгновенного ускорения, следовательно:
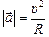 . (12.11)
. (12.11)
Итак, модуль мгновенного ускорения мы нашли. Осталось только выяснить его направление.
Рассмотрим DВСD. Если Dj ® 0, то два остальных угла этого треугольника: ÐСВD = ÐСDВ ® 90o, так как сумма углов треугольника равна 180о. А значит, BD^BС, следовательно, D  ^
^  к.
к.
Вектор  к направлен по касательной к окружности, а перпендикуляром к касательной в точке касания является радиус окружности. Получается, что вектор D
к направлен по касательной к окружности, а перпендикуляром к касательной в точке касания является радиус окружности. Получается, что вектор D  должен быть направлен по радиусу, т.е. к центру окружности.
должен быть направлен по радиусу, т.е. к центру окружности.
Вектор ускорения  , как мы знаем, сонаправлен с вектором D
, как мы знаем, сонаправлен с вектором D  :
: 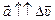 , следовательно, мгновенное ускорение направлено к центру окружности. Поэтому ускорение, с которым материальная точка равномерно движется по окружности, еще называется центростремительным (оно как бы стремится к центру).
, следовательно, мгновенное ускорение направлено к центру окружности. Поэтому ускорение, с которым материальная точка равномерно движется по окружности, еще называется центростремительным (оно как бы стремится к центру).
Итак, мы выяснили, что если материальная точка движется по окружности радиуса R равномерно со скоростью υ, то ее мгновенное ускорение в любой момент времени направлено к центру окружности и по модулю равно 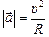 .
.
Дата добавления: 2016-04-11; просмотров: 975;
