Связь между скоростью

И угловой скоростью

Пусть материальная точка движется по окружности радиуса R равномерно со скоростью υ.Спрашивается: чему равна его угловая скорость?

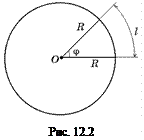
Пусть за время t радиус, соединяющий нашу материальную точку с центром окружности, повернулся на угол j и материальная точка при этом прошла расстояние, равное длине дуги l (рис. 12.2). Тогда угол j, измеренный в радианах, равен:

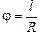, (1)

а угловая скорость по формуле (12.4) равна

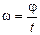. (2)

Подставив значение j из (1) в (2), получим:

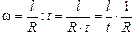. (3)

Отношение l/t – это скорость движения материальной точки по окружности: 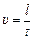. Поэтому из (3) следует:

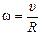. (12.5)

Отсюда

υ = wR. (12.6)

Из формулы (12.6) следует, что скорость υ линейно зависит от ра­диуса окружности, т.е. является линейной функцией радиуса υ = wR точно так же, как у является линейной функцией х, если у = kх. Поэтому скорость υ, с которой материальная точка движется по ок­ружности, называют еще линейной скоростью.

Заметим, что если в формуле (12.5) [υ] = м/с и [R] = м, то [w] = рад/с, поскольку угол j, вычисленный по формуле (1), измеряется в радианах.

Связь между периодом