Метод малых перемещений
ДВИЖЕНИЕ С КИНЕМАТИЧЕСКИМИ
СВЯЗЯМИ
Если два движущихся тела (шарика, лодки, автомобиля) в прямом смысле этого слова связаны чем-нибудь (веревкой или жестким стержнем) между собой, то такое движение называется движением с кинематическими связями.
Почему с кинематическими? Да потому, что при таком движении кинематические величины этих тел: пути, перемещения, скорости, ускорения, – связаны между собой.
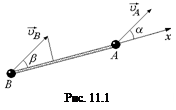 Рассмотрим, например, движение двух шариков А и В, скрепленных жестким стержнем (рис. 11.1). Скорости шариков
Рассмотрим, например, движение двух шариков А и В, скрепленных жестким стержнем (рис. 11.1). Скорости шариков 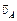 и
и 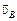 , вообще говоря, могут быть и не равны между собой:
, вообще говоря, могут быть и не равны между собой: 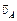 ¹
¹ 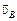 , но длина стержня (если он жесткий) АВ в процессе движения меняться не может. А отсюда вытекает кинематическая связь между величинами
, но длина стержня (если он жесткий) АВ в процессе движения меняться не может. А отсюда вытекает кинематическая связь между величинами 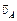 и
и 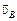 .
.
В самом деле, если мы введем ось х, направленную вдоль стержня, то проекции векторов 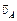 и
и 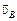 на эту ось должны быть равны:
на эту ось должны быть равны:
υАх = υВх. (11.1)
(Иначе точки А и В либо сближались, либо удалялись друг от друга.) Отсюда следует
υАcosa = υВcosb. (11.2)
Разберем решение нескольких типовых задач.
Неразрывность стержня (нити)
Задача 11.1. Стержень длиной l = 1,0 м шарнирно соединен с муфтами А и В, которые перемещаются по двум взаимно перпендикулярным рейкам (рис. 11.2,а). Муфта А движется с постоянной скоростью υА = 30 см/с. Найти скорость υВ муфты В в момент, когда угол ОАВ = 60°.
| l = 1,0 м υА = 30 см/с ÐОАВ = a = 60° | Решение. Введем ось х, сонаправленную с отрезком ВА (рис. 11.2,б). Тогда согласно формуле (11.1) υВх = υАхÞυВcos(90°– a) = υАcosa Þ |
| υВ = ? |
Þ υВsina = υАcosa Þ υВ = υА(cosa/sina) = υАctga,
υВ = 30 см/с × ctg60° » 17 см/с.
а) 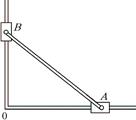 б)
б) 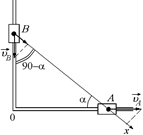
Рис. 11.2
Ответ: υВ = υАctga » 17 см/с.
СТОП! Решите самостоятельно: А1–А3, В1, В3, В5.
Метод малых перемещений
Задача 11.2. В конструкции, показанной на рис. 11.3,а, левый конец веревки закреплен. По известной скорости υА точки А определить скорость точки В в момент, когда нить образует с вертикалью угол a.
а) 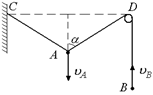 б)
б) 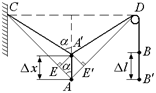
Рис. 11.3
| υА, a | Решение. Пусть за малое время Dt точка А опустилась вниз на малое расстояние Dх ® 0, а точка В поднялась на малое расстояние Dl (рис. 11.3,б). Тогда |
| υВ = ? | |
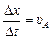 ,
, 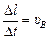 .
.
Пусть Dх нам известно, найдем из геометрических соображений Dl. Опустим из точки А¢ перпендикуляры А¢Е ^СА и А¢E¢^ AD. В силу малости величины Dх можно считать, что СА¢ = СЕ, а DA¢ = =A¢Е. Тогда удлинение нити слева от блока D равно сумме отрезков: ЕА + АЕ¢, каждый из которых равен ЕА = АЕ¢ = АА¢cosa = =Dxcosa. Именно на столько укоротилась нить справа от блока D, ведь общая длина нити неизменна: Dl = EA + AE¢ = 2Dxcosa.
Итак, Dl = 2Dxcosa 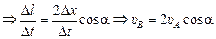 .
.
Ответ: 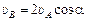 .
.
СТОП! Решите самостоятельно: В7, В8, С1, С2.
Движение теней
Задача 12.3. Человек высоты h проходит в стороне от фонаря, висящего на высоте Н над землей. Найти величину и направление скорости перемещения по земле тени от головы человека, если он идет со скоростью υ.
| h, H, υ | 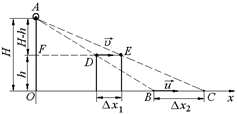 Рис. 11.4 Рис. 11.4
|
| и = ? | |
Решение. Пусть за малое время Dt ® 0 голова человека переместилась на расстояние Dx1 вправо из точки D в точку Е (рис. 11.4). Тогда тень от головы переместилась на Dx2 из точки В в точку С. Учтем, что 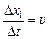 ,
, 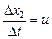 . Найдем связь между Dx1 и Dx2.
. Найдем связь между Dx1 и Dx2.
Рассмотрим DADE и DАВС: они подобны, тогда
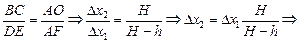
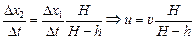 .
.
Ответ: тень движется вправо со скоростью 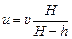 .
.
СТОП! Решите самостоятельно: С4, С5, D1.
Дата добавления: 2016-04-11; просмотров: 5908;
