И периодом вращения

Пусть период вращения материальной точки по окружности равен Т. Спрашивается, какова частота вращения? Согласно формуле(12.1) 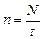. За время t = Т материальная точка совершаетN = 1 оборот. Следовательно:

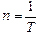. (12.2)

Из формулы (12.2) следует, что:

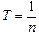. (12.3)

Угловая скорость

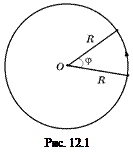
Пусть материальная точка равномерно движется по окружности и пусть за время t радиус окружности, соединяющий центр окружности с движущейся точкой, повернулся на угол j (рис. 12.1).

Физическая величина, равная отношению угла поворотаjко времени поворотаt,называется средней угловой скоростьюw:

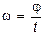. (12.4)

Ясно, что при равномерном движении w – величина, не зависящая от времени.

Заметим, что угол, измеренный в радианах, – это отношение дли­ны дуги к длине радиуса: [j] = 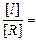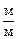= 1, т.е. с точки зрения физики угол – величина безразмерная: [j] = 1.

Читатель: А если угол измеряется в градусах, тогда это размерная ве­личина?

Автор: Тоже безразмерная! Ведь для того чтобы величину угла, измеренного в радианах, перевести в градусы, достаточно умножить значение угла в радианах на число 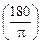. Ясно, что при перемножении двух безразмерных величин получается безразмерная величина: [j] = 1. Поэтому размерность w равна

.

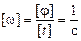Однако для удобства в условиях задач обычно пишут в качестве раз­мерности w не 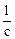, а рад/с. Но при проверке размерности результата надо помнить, что 1 рад = 1, то есть [j] = рад = 1 и 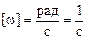. При желании можно измерять w и в градусах в секунду: [w] = град/с.