Нормальное распределение

Нормальным называют распределение вероятностей непрерывной случайной величины X, плотность которого имеет вид

,

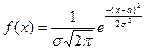где a-математическое ожидание, 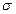- среднее квадратичное отклонение X. Вероятность того, что Х примет значение, принадлежащее интервалу (α,β):

,

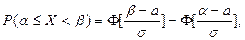где 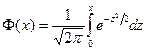- функция Лапласа.

Пример 99. Математическое ожидание и среднее квадратическое отклонение нормально распределенной случайной величины Х примет значение: а) в интервале (-1,2); б) меньше -1; в) больше 2; г) отличающееся от своего среднего значения по абсолютной величине не больше, чем на 1.

Решение. По условию задачи a=0, σ=2, тогда:

а)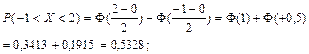

б)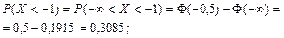

в)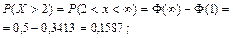

г)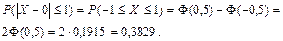

Здесь значения функции Φ(x) были найдены по таблице и учитывалось, что Φ(-x) = -Φ(x), а .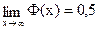

100. Плотность распределения ошибки выходного параметра РЭА имеет вид

.

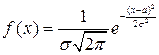Сборочные операции изменяют числовые характеристики распределения, не изменяя закона. Что больше увеличивает вероятность появления брака: систематическое смещение значения ошибки выходного параметра на а единиц или увеличение дисперсии ошибки на эти же а единиц?

101. Математическое ожидание и дисперсия случайного напряжения с нормальным распределением равны 10 В и 25 В² соответственно. Какова вероятность того, что измеренное значение напряжения

а) будет больше 0?

б) будет находиться в интервале от 0 до математического ожидания?

в) будет в два раза больше математического ожидания?

102. Широко распространенный метод обнаружения сигнала в присутствии шума заключается в установлении определенного порогового уровня, с кото­рым производится сравнение результатов измерения напряжения, включающего полезный сигнал и шум. Если установленный порог превышается, то считают, что полезный сигнал присутствует. Естественно, иногда и при отсутствии сиг­нала шум превосходит этот порог, и такая ситуация называется ложной тре­вогой. Желательно, чтобы вероятность ложной тревоги была ничтожно мала. В то же время необходимо, чтобы результат любого измерения, проведенного при наличии сигнала, смешанного с шумом, с большой вероятностью превосхо­дил установленный порог. Она называется вероятностью правильного обнаружения и должна как можно меньше отличаться от 1. Пусть шум характеризуется нормальным распределением с нулевым математическим ожиданием и дисперсией 1В², а установленный порог равен 5 В.

а) Определите вероятность ложной тревоги.

б) Определите вероятность правильного обнаружения сигнала величиной 8 В в присутствии шума с заданными выше параметрами.

103. Математическое ожидание и среднее вадратическое отклонение нормально распределенной случайной величины X соответственно равны 20 и 5. Найти вероятность того, что в результате испытания X примет значение, заключенное в интервале (15, 25).

104. Производится взвешивание некоторого вещества без систематических ошибок. Случайные ошибки взвешивания подчинены нормальному закону со средним квадратическим отклонением σ = 20 г. Найти вероятность того, что взвешивание будет произведено с ошибкой, не превосходящей по абсолютной величине 10 г.

105. Случайные ошибки измерения подчинены нормальному закону со средним квадратическим отклонением σ = 20 мм и математическим ожиданием а = 0. Найти вероятность того, что из трех независимых измерений ошибка хотя бы одного не превзойдет по абсолютной величине 4 мм.

106. Вывести «правило трех сигм»: вероятность того, что абсолютная величина отклонения нормально распределенной случайной величины будет меньше утроенного среднего квадратического отклонения, равна 0,9973. 107. Станок-автомат изготовляет валики, причем контролируется их диаметр X. Считая, что X—нормально распределенная случайная величина с математическим ожиданием а=10мм и средним квадратическим отклонением σ = 0,1 мм, найти интервал, симметричный относительно математического ожидания, в котором с вероятностью 0,9973 будут заключены диаметры изготовленных валиков.