Классическое определение вероятности

При классическом определении вероятность появления события А вычисляется по формуле:

,

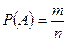где m – число элементарных исходов испытания, благоприятствующих появлению события А; n – общее число равновозможных элементарных исходов испытания.

Пример 1. Брошены 2 игральные кости. Найти вероятность того, что сумма очков на выпавших гранях четная, причем на грани хотя бы одной из костей появится шестерка.

Решение. Общее количество равновозможных элементарных исходов испытания найдем по принципу умножения: n= 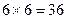. Благоприятствующим интересующему нас событию являются следующие исходы: 1) 6, 2; 2) 6, 4; 3) 6, 6; 4) 2, 6; 5) 4, 6. Здесь первым записано число очков, выпавших на первой кости, вторым – число очков на второй кости. Таким образом, число благоприятных исходов m=5, следовательно

Пример 2. В конверте 10 карточек с номерами 1, 2, …10. Наудачу извлечены 6 карточек. Найти вероятность того, что среди извлеченных окажутся: а) карточка №1, б) карточки №1 и №2.

Решение. Общее число равновозможных элементарных исходов испытания равно числу наборов по 6 карточек из 10, отличающихся хотя бы одной карточкой, т.е. . Найдем число благоприятных исходов: в наборе есть карточка №1, а остальные 5 имеют другие номера, следовательно, их можно извлечь способами. Тогд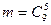а

, а

б) Поскольку среди отобранных в этом случае есть карточки №1 и №2, то из оставшихся 8 извлекаются 4, следовательно

, а

Пример 3. Из 10 букв разрезной азбуки составлено слово «математика». Ребенок, не умеющий читать, рассыпал эти буквы, а затем собрал в произвольном порядке. Найти вероятность того, что у него снова получилось слово «математика».

Решение. Общее число исходов испытания равно числу перестановок 10 букв, т.е. n=P =10!
Если бы слово состояло из разных букв, то благоприятным был один исход. Но в заданном слове «м» повторяется 2 раза, «а» - 3 раза, «т» - 2 раза, поэтому возможны их перестановки, при которых слово не изменяется. Поэтому

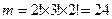, а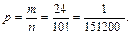

4. В коробке 6 одинаковых занумерованных кубиков. Наудачу по одному извлекают все кубики. Найти вероятность того, что номера извлеченных кубиков появятся в возрастающем порядке.

5. В ящике содержится 15 деталей, среди которых 10 окрашенных. Сборщик наудачу извлекает 3 детали. Найти вероятность того, что извлеченные детали окажутся окрашенными.

6. Устройство состоит из 5 элементов, из которых 2 изношены. При включении устройства случайным образом включаются 2 элемента. Найти вероятность того, что включенными окажутся неизношенные элементы.

7. На складе имеется 15 кинескопов, причем 10 из них изготовлены Воронежским заводом. Найти вероятность того, что среди 5 наудачу взятых кинескопов - 3 кинескопа воронежского завода.

8. Наудачу выбирается пятизначное число. Какова вероятность следующих событий: А={число одинаково читается как слева направо, так и справа налево (как, например, 13531)}, В={число кратно пяти}, С={число состоит из нечетных цифр}.

9. Подбрасываются две игральные кости. Найти вероятности следующих событий: А={числа очков на обеих костях совпадают}, В={число очков на первой кости больше, чем на второй}, С={сумма очков четна}, D={сумма очков больше двух}, E={сумма очков не меньше пяти}, F={хотя бы на одной кости появится цифра шесть}, G={произведение выпавших очков равно шести}.

10. Пяти полевым радиостанциям разрешено во время учений работать на шести радиоволнах. Выбор волны на каждой радиостанции производится наудачу. Найти вероятности следующих событий: A={при одновременной работе всех пяти радиостанций хотя бы две волны не совпадут}, В={будут использованы различные радиоволны}.

11. На шахматную доску случайным образом ставят две ладьи – белую и черную. Какова вероятность, что ладьи не побьют друг друга?

12. Среди кандидатов в студенческий совет факультета 3 первокурсника, 5 второкурсников и 7 третьекурсников. Из этого состава наудачу выбирают пять человек на предстоящую конференцию. Найти вероятности следующих событий: А={будут выбраны одни третьекурсники}, В={все первокурсники попадут на конференцию}, С={не будет выбрано ни одного второкурсника}, D={будет выбран следующий состав: 1 первокурсник, 2 второкурсника и 2 третьекурсника}.

13. Группа, состоящая из 8 человек, занимает места с одной стороны прямоугольного стола. Найти вероятность того, что два определенных лица окажутся рядом, если
а) число мест равно 8;
б) число мест равно 12.

14. Телефонная книга раскрывается наудачу и выбирается случайный номер телефона. Считая, что телефонные номера состоят из 7 цифр, причем все комбинации цифр равновероятны, найти вероятности следующих событий: А={четыре последние цифры телефонного номера одинаковы}, В={все цифры различны}, С={номер начинается с цифры 5}, D={номер содержит три цифры 5, две цифры 1 и две цифры 2}.

15. Шесть пассажиров поднимаются на лифте семиэтажного дома. Считая, что движение лифта начинается с цокольного этажа, найти вероятности следующих событий: А={на первых трех этажах не выйдет ни один из пассажиров}, В={все пассажиры выйдут на первых шести этажах}, С={на пятом, шестом и седьмом этажах выйдут по два пассажира}, D={все пассажиры выйдут на одном этаже}.