Числовые коды, представление отрицательных чисел

Кодом называется любое обозначение, отличное от общепринятого. Общепринято, например, положительные числа отмечать знаком «+» (или вообще не указывать знак), а отрицательные числа отмечать знаком «-». Числа разного знака необходимо уметь изображать состояниями элементов цифровой электроники. Для изображения знака числа вводится дополнительный знаковый разряд, причем состоянию «0» этого разряда соответствует знак «+», а состоянию «1» — знак «-».Такое изображение чисел со знаком называется прямым кодом [Х]_пр числа X. Поскольку разрядность цифровых вычислительных устройств обычно кратна одному байту, то под знаковый разряд отводится крайний левый бит в старшем байте. Таким образом, если для представления чисел в цифровом устройстве предусмотрен один байт (8 бит), то знаковым будет восьмой разряд байта, а оставшиеся семь будут отведены для значащих разрядов числа, что сделает возможным оперировать с целыми числами в диапазоне от -127 до +127. Если же разрядность цифрового устройства 2 байт (16 бит), то знаковым будет шестнадцатый разряд, а значащими окажутся разряды с первого по пятнадцатый и т.д. Таким образом, прямой код целого Числа образуется по правилу: если число X положительно, то [X]_пр ⁼ = 0, Х_ь Х₂, ..., Х_песли число Xотрицательно, то [Х]_пр= 1, Х_ъ Х₂,..,, Х_тгде п = 8, 16 и т.д.

Обратный код числа образуется инвертированием всех разрядов прямого кода числа, кроме знакового. Операция инвертирования

заключается в поразрядной замене нулей на единицы и единиц на нули. Таким образом, если число X положительно, то [Х]_о6р = (0,`Х <sub>1</sub> `,Х₂,...,`Х<sub>п</sub>; если число X отрицательно, то [Х]<sub>обр</sub> = 1, `Х₁,` Х<sub>2</sub>,...`,Х_п где п = 8, 16 и т.д. Как известно, правила сложения чисел отличаются от правил вычитания. Чтобы выполнить эти операции необходимо иметь два самостоятельных устройства: сумматор и вычитатель. Но оказалось, что можно обойтись только одним устройством — сумматором, если изображать числа, участвующие в операции, в дополнительных кодах. Дополнительный код положительного числа сое впадает с прямым кодом этого числа.

Дополнительный код отрицательного числа получается следующим образом:

• записывают обратный код исходного числа;

• прибавляют единицу к младшему разряду. Дополнительный код числа будем обозначать как [Х]_доп. При этом если в результате вычитания в знаковом разряде получается единица, то результат отрицательный и представлен в дополнив тельном коде, а если нуль — то положительный и представлен ж прямом коде. В табл. 2 приводится пример кодов некоторых положительных и отрицательных десятичных чисел.

В процессе выполнения арифметических операций необходимо следить за тем, чтобы промежуточные и конечные результаты не выходили бы за пределы отведенной разрядной сетки. Для этих целей используют так называемый модифицированный дополнительный код [X]^м_доп. Согласно этому коду под знаковый отводится не один, а два разряда. Правила перевода в модифицированный дополнительный код такие же, как и в обычный дополнительный код. Отличие состоит в том, что в модифицированном дополнительном коде положительному числу в знаковых разрядах соответствуют два нуля, а отрицательному числу — две единицы. При этом если в результате некоторой арифметической операции в| знаковых разрядах произошло чередование нуля и единицы (возникли комбинации 01или 10),

Таблица 2

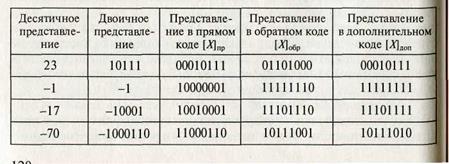
то имело место переполнение разрядной сетки и результат следует считать неверным.

В принципе логика выполнения арифметических операций в двоичной системе счисления наиболее проста. Это наглядно на примере сравнения таблиц умножения десятичных цифр с одной единственной таблицей умножения двоичных цифр, имеющей вид: 0x0 = 0; 0x1=0; 1x0 = 0; 1x1 = 1.

Необходимо особо подчеркнуть, что правила выполнения арифметических операций над многоразрядными числами, представленными в позиционных системах счисления с различными основаниями, одни и те же. Отличие составляют лишь правила сложения и умножения одноразрядных чисел (для каждой системы счисления существуют свои таблицы умножения и сложения).

В цифровых вычислительных устройствах для реализации операций быстрого деления и умножения числа на 2ⁿ, где п — целое положительное число, используются операции сдвига двоичного кода числа вправо или влево. Сдвинуть двоичный код влево на один разряд соответствует умножению его на 2, а вправо — делению на 2. Например, десятичному числу 8 соответствует двоичный код 00001000, а десятичному числу 16, равному удвоенному значению 8, двоичный код 00010000. Очевиден сдвиг кода влево на один разряд. Десятичному же числу 4, вдвое меньшему 8, соответствует двоичный код 00000100. Налицо сдвиг вправо на один разряд двоичного кода. При проектировании цифровых умножителей на произвольный коэффициент используется алгоритм традиционного умножения столбиком.

9. Определение функции алгебры логики

Для анализа и синтеза цифровых электронных схем широко используется математический аппарат алгебры логики, или булевой алгебры, разработанной в середине XIX в. ирландским математиком Дж. Булем. Основным понятием алгебры логики является понятие переключательной функции, илибулевой функции алгебры логики (ФАЛ). Функцией алгебры логики и переменных называет­ся такая функция, которая принимает только два возможных значения (0 или 1), как и переменные, от которых эта функция зависит. Для п переменных возможно 2ⁿ различных значений переключательной функции f Если заданы все 2ⁿ значений функции, то она называется полностью определенной. Если же часть значений функции f не задана, то такая функция носит название неопределенной или частично определенной.

ФАЛ задаются таблично (в виде так называемых таблиц истинности), аналитически (в виде алгебраических выражений), в виде последовательности десятичных чисел или в виде кубических комплексов. В табл. 3 приведен пример табличного задания произвольной функции трех переменных f=f(A, В, С).

Таблица 3

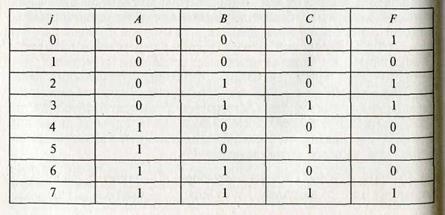
Конкретная комбинация значений аргументов носит название. набора. Каждый набор имеет индексу, численно равный десятичному эквиваленту двоичного числа.

ФАЛ от одной и двух переменных принято называть элементарными. Эти функции имеют специальные названия и обозначения и используются при воспроизведении более сложных логических функций. В табл..4 приведены все возможные переключательные функции двух переменных.

Для аналитической записи переключательных функций используются вспомогательные функции, называемые конституентой единицы и конституентой нуля. Конституентой единицы п переменных называется такое булево произведение (конъюнкция) этих переменных, в которое каждая переменная входит только один раз в прямой или инверсной форме. Переменная, принимающая на данном наборе единичное значение, записывается в конституенте единицы в прямом виде, а отрицательное — в инверсном виде. Отличительной особенностью конституенты единицы явля- ется то, что она равна «1» только на одном вполне определенном наборе значений переменных. Будем обозначать конституенту единицы символом m_j, где индекс j указывает на номер набора, на котором конституента единицы становится равной «1». Аналогично конституента нуля есть булево сложение (дизъюнкция) п логических переменных, которое обращается в «0» лишь при одном наборе аргументов. При этом в прямом виде в конституенте нуля будет записываться переменная, принимающая на данном наборе нулевое значение, а в инверсном — единичное значение.

Аналитическая запись функции осуществляется по таблице истинности. Непосредственно из данных таблицы находится так

Таблица 4

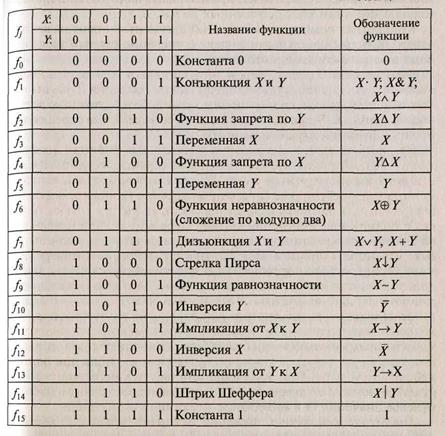
называемая совершенная дизъюнктивная нормальная форма булевой функции (СДНФ) по выражению:

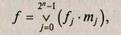
Где f_j — значение функции на j-м наборе; т_} — конституента единицы, равная «1» только на одном j-м наборе; v — символ логического сложения (дизъюнкции), аналогичный символу алгебраического сложения Σ.

Для записи выражений в совершенной конъюктивной нормальной форме (СКНФ) используют формулу:

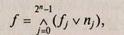
Где f_j— значение функции на j-м наборе; n_j — конституента нуля, Равная «0» только на одном j-м наборе; ^ — символ логического произведения (конъюкции), аналогичный символу (х) алгебраического произведения.

Для выражения ФАЛ от многих переменных достаточно иметь ограниченное число разнотипных элементарных переключательных функций, называемое системой. Как показано выше, любая функция алгебры логики может быть записана в виде СДНФ или СКНФ. Следовательно, любую функцию аргументов можно представить с помощью системы только из трех элементарных функций: инверсия, дизъюнкции и конъюнкции.

Система функций алгебры логики называется функционально полной, если любая функция от произвольного числа аргументов п может быть представлена с помощью этих функций. Полная система функций называется базисом. Базисом называется такой базис, для которого удаление хотя бы одной из функций, образующих этот базис, превращает систему функций в неполную. Так, полная система из дизъюнкции, конъюнкции и инверсии может быть сокращена, поскольку с помощью формул де Моргана можно представить либо конъюнкцию через инверсию и дизъюнкцию, либо дизъюнкцию через инверсию и конъюнкцию. Таким образом, базис из дизъюнкции, конъюнкции и инверсии не является минимальным. Поскольку ни дизъюнкция, ни конъюнкция не могут быть выражены через инверсию и наоборот, то базисы, состоящие из инверсии и дизъюнкции и из инверсии и конъюнкции, являются минимальными. Возможны различные базисы и минимальные базисы, отличающиеся числом входящих в них функций и их видом. Приведем примеры функционально полных систем:

• конъюнкция, дизъюнкция, инверсия;

• конъюнкция, инверсия;

• дизъюнкция, инверсия;

• стрелка Пирса;

• штрих Шеффера.

Выбор минимального базиса связан с выбором стандартного набора логических элементов, из которых будет строиться конкретное цифровое устройство. Очевидно, что уменьшение числа функций, входящих в базис, соответствует уменьшению числа различных логических элементов, принятых за стандартные. Однако уменьшение типов стандартных элементов может привести к увеличению их общего числа. Таким образом, сложность цифрового устройства зависит не только от вида реализуемой функции, но и от вида функций, выбранных в качестве базиса.

Контрольные вопросы

1.Какими параметрами характеризуются одиночный импульс и импульсная последовательность?

2.Какие методы применяются при анализе линейных импульсных цепей?

3.В каких случаях RС-цепь является интегрирующей или разделительной?

4.Как определяется качество интегрирования и от чего оно зависит?

5.От чего зависит «завал» вершины импульса в разделительной цепи?

6.Дайте определение системы счисления и приведите примеры используемых в цифровой технике систем счисления.

7.Отнимите из числа 57₁₀ число 83₁₀ и из числа 83₁₀ число 57₁₀ по правилам двоичной арифметики, используя дополнительные коды иоперацию сложения.

8.Дайте определение функции алгебры логики. Приведите различные формы записи для произвольной логической функции трех переменных.

9. Что такое числовой код?

10. Что такое СКНФ и СДНФ?