П. 2.7. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ НЕПРЕРЫВНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ

Математическим ожиданием непрерывной случайной величины, возможные значения которой принадлежат интервалу [a, b], называется определенный интеграл 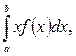т.е.

М (Х) = 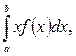(2.7.1)

Если возможные значения случайной величины принадлежат всей числовой оси, то

М (Х) =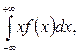

при этом предполагается что интеграл 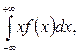существует.

По аналогии с дисперсией дискретной случайной величины определяется дисперсия непрерывной случайной величины:

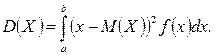(2.7.2)

Если возможные значения принадлежат всей оси Ох, то

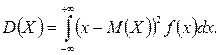
Свойства М(х) и D(x) формулируются так же, как и соответствующие свойства для дискретной величины.

Величину σ_x = 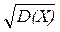называют средним квадратическим отклонением случайной величины или стандартом, σ_x имеет ту же размерность, что и сама случайная величина. Из формулы (12.7.2) нетрудно получить более удобные формулы для вычисления дисперсии, а именно:

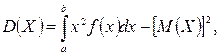(2.7.3)

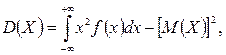(2.7.4)

Пример. Случайная величина х задана функцией распределения

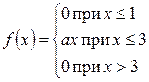
Найдите: 1) коэффициент а; 2) М(Х); 3) D(X).

Решение. Используя формулу (2.6.4), получаем

1.

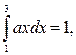
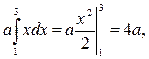
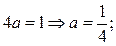
2.

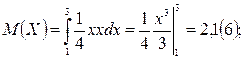
3.

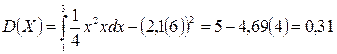
П. 2.8. ПРИМЕРЫ, ПРИВОДЯЩИЕ К ПОНЯТИЮ

НОРМАЛЬНОГО РАСПРЕДЕЛЕНИЯ.