П. 2.9. ВЕРОЯТНОСТЬ ПОПАДАНИЯ

НОРМАЛЬНО РАСПРЕДЕЛЕННОЙ СЛУЧАЙНОЙ

ВЕЛИЧИНЫ В ЗАДАННЫЙ ИНТЕРВАЛ.

ПРАВИЛО ТРЕХ СИГМ

Пусть дан интервал α<Х<β. Вероятность того, что случайная величина, подчиненная нормальному закону с параметрами а и σ, попадает в этот интервал, равна

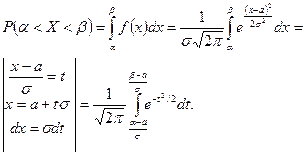
Учитывая, что

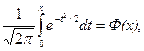
Найдем

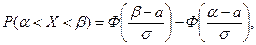(2.9.1)

где Ф (х) - функция Лапласа,

Рассмотрим частный случай. Пусть необходимо найти вероятность попадания случайной величины в интервал, симметричный относительно математического ожидания. Учитывая (2.9.1), имеем

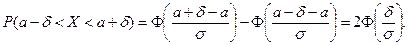
Так как 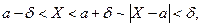то

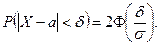(2.9.2)

Вычислим теперь вероятности:

1) 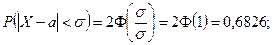(2.9.3)

2) 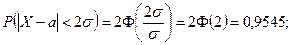(2.9.4)

3) 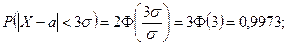(2.9.5)

Результаты вычислений по формуле (2.9.5) показывают, что вероятность отклонения случайной величины X от М(Х) меньше чем на 3σ близка к 1.

Правило трех сигм. Практически достоверно, что при однократном испытании отклонение нормально распределенной случайной величины от ее математического ожидания не превышает утроенного среднего квадратического отклонения.

Это правило часто используется в математической статистике.