Проверка однородности выручки, получаемой от российского экспорта основных видов продукции
Для оценки однородности средних значений независимых нормально распределенных величин, дисперсии которых равны (однородны), но неизвестны, может быть использован критерий Аббе, статистика которого задается отношением
 . (1.18)
. (1.18)
Проверяется нуль-гипотеза Н0: m*1(x) = m*2(x) = m*3(x) = m*4(x) при альтернативе Н1: |m*i+1(x) – m*i (x)| > 0.
Если найденное значение q-статистики превышает критическое, то гипотеза о равенстве средних отвергается.
Пример 1. Требуется проверить гипотезу об однородности вкладов, приведенных в табл. 7, видов продукции в выручку от экспорта (данные по четырем федеральным округам РФ) в предположении, что известны только mi*(x) – средние значения выручки [17], а другой информации нет.
Таблица 7
Экспорт некоторых видов продукции России в 2000 г. по федеральным округам, млн долл
| Федеральные округа | Нефтехимические товары | Черные и цветные металлы | Машиностроительная продукция | Древесина и изделия из нее |
| Северо-западный | 3,0 | 2,3 | 1,5 | 1,6 |
| Южный | 1,6 | 0,6 | 0,4 | 0,0 |
| Сибирский | 2,3 | 5,7 | 0,5 | 1,0 |
| Дальневосточный | 1,0 | 0,3 | 0,6 | 0,5 |
| m*i (x) | 1,98 | 2,23 | 0,75 | 0,78 |
| D*i (x) | 0,7 | 6,1 | 0,3 | 0,5 |
Значения средних представляют в виде вариационного ряда: 0,75; 0,78; 1,98; 2,23, со средним 1,43 и вычисляют q-статистику:
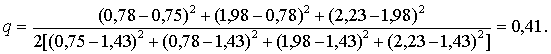
В соответствии с табл. 6 приложения значение q-статистики при n = 4 уровне значимости α= 0,05 составляет qкр = 0,3902 < q =
= 0,41, поэтому гипотеза о равенстве средних отвергается.
Следовательно, вклад в экспортную выручку различных видов продукции по указанным районам неодинаков: на первом месте – нефтехимические товары, на втором – черные и цветные металлы, и так далее.
Однако при вычислении q-статистики Аббе используется не вся информация об объектах, поэтому для парного сравнения средних используют критерий Стьюдента (табл. 7 приложения), тогда его статистика:
 (1.19)
(1.19)
где 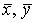 – исследуемые средние значения; D*(x3), D*(x4) – оценки дисперсий случайных величин; n, m – объемы выборок; (n – 1),
– исследуемые средние значения; D*(x3), D*(x4) – оценки дисперсий случайных величин; n, m – объемы выборок; (n – 1),
(m – 1)– числа степеней свободы оценок дисперсий.
Проверяется нулевая гипотеза Н0: 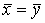 при альтернативной Н1:
при альтернативной Н1: 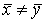 при условии однородности оценок дисперсий и нормального распределения X и Y. Нулевая гипотеза отвергается, если |tнабл.| > tдвуст.кр (α/2; k), где a – уровень значимости, k – число степеней свободы, k = n + m – 2.
при условии однородности оценок дисперсий и нормального распределения X и Y. Нулевая гипотеза отвергается, если |tнабл.| > tдвуст.кр (α/2; k), где a – уровень значимости, k – число степеней свободы, k = n + m – 2.
Пример 2. Оценить с помощью t-критерия однородность средних значений экспортной выручки для трех вариантов:
1) от машиностроительной продукции и древесины и изделий из нее при выполнении условия однородности оценок D*(x3) и D*(x4);
2) от нефтехимических товаров, черных и цветных металлов;
3) от нефтехимических товаров и древесины и изделий из нее.
Решение. 1. В соответствии с формулой
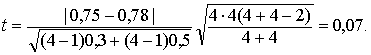
Найденное значение t-статистики меньше критического (табл. 7, приложения);
tнабл.= 0,07 < tдвуст.кр (0,1/2; 6) = 1,9432,
поэтому гипотеза о равенстве выручки по четырем районам РФ от машиностроительной продукции и от древесины и изделий из нее не отвергается.
2. Прежде, чем вычислить значение t-статистики для второго варианта, необходимо проверить однородность оценок дисперсий c помощью F-статистики (табл. 10 приложения):
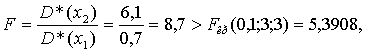
т. е. оценки дисперсий для исследуемых товаров X1и X2 неоднородны, t-критерий не позволяет решать задачу об однородности m*(x1) и m*(x2).
3. Здесь очевидно, что оценки дисперсий однородны, значение t-статистики
 ,
,
поскольку tнабл. = 2,19 > tдвуст.кр (0,1/2; 6) = 1,9432 (табл. 7 приложения). Средние значения товаров X1 и X4 неоднородны, экспортная выручка от товаров нефтехимии больше, чем от древесины и изделий из нее. Все это согласуется с результатом, полученным при использовании критерия Аббе, который дает положительный ответ по поводу однородности средних значений только в случае, когда все средние однородны, но, если хотя бы одно значение неоднородно с каким–либо другим, то и ответ будет отрицательным.
Однородность средних для зависимых выборок проверяется с помощью d-статистики. Проверяется нулевая гипотеза
Н0 : М*(X) = M*(Y) при конкурирующей Н0: М*(X) ≠ M*(Y).
Пример 3. Средний балл успеваемости группы ИЭ-00 по математике в первом семестре по результатам экзаменационной сессии составил 3,43, во втором – 3,52, в третьем – 3,65, в четвертом – 3,74. Оценить однородность средних баллов, полученных студентами группы ИЭ-00 в 1-м и 4-м семестрах по математике во время экзаменационных сессий (табл. 8).
Таблица 8
Баллы, полученные студентами группы ИЭ-00 по математике в 1-м и 4-м семестрах
| Семестр | Балл | ||||||||||||||||||||||
Решение. Выборки зависимы, так как баллы 1-го и 4-го семестров в каждом столбце получены одним и тем же студентом и в силу этого являются попарно зависимыми.
Вычисляется среднее значение разностей баллов
d* = Σdi /n,
где di = xi – yi; xi, yi – баллы студентов, полученные ими в 1-м и 4-м семестрах соответственно, n – число студентов в группе.
d1 = 3 – 4 = – 1; d2 = 3 – 3 = 0;…; d5 = 3 – 4 = – 1;
d6= 4 – 5 = – 1;…; d9 = 3 – 4 = – 1; d10 = 5 – 4 = 1;
d15 = 3 – 4 = – 1;…; d20 = 4 – 5 = – 1; d21 = 3 – 4 = – 1;
d22 = 3 – 3 = 0; d23 = 4 – 5 = –1.
Σdi = – 1 – 1 – 1 – 1 + 1 – 1 –1 – 1 – 1 = – 7;
d* = –7 / 23 = – 0,304.
Сумма квадратов разностей
Σd2i = (–1)2 + (–1)2 +(–1)2 + (–1)2 + (+1)2 + (–1)2 +(–1)2 + (–1)2 + (–1)2 = 9.
Среднее квадратическое отклонение разностей
Sd = 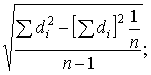 Sd =
Sd = 
Наблюденное значение Т-статистики
Тнабл = d*n0,5/Sd = – 0,304·230,5/0,559 = – 2,6081.
Поскольку абсолютное значение Т-статистики больше, чем критическое значение tдвуст.кр.(0,10; 32) = 1,70 (табл. 7 приложения), средние баллы 1-го и 4-го семестров неоднородны, поэтому можно считать, что от 1-го к 4-му семестру имеет место небольшое, но значимое повышение успеваемости.
Дата добавления: 2016-03-27; просмотров: 729;
