Основные свойства определенного интеграла
1. Определенный интеграл с равными пределами интегрирования равен нулю
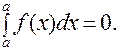
|
2. Если поменять пределы интегрирования местами, определенный интеграл изменит знак
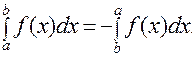
|
3. Для любых чисел а, b и с справедливо равенство
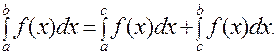
|
4. Постоянный множитель, не равный нулю, можно выносить за знак определенного интеграла
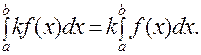
|
5. Определенный интеграл от алгебраической суммы двух функций равен алгебраической сумме интегралов от этих функций
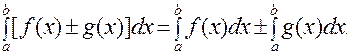
|
6. Если для всех 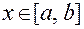 справедливо неравенство
справедливо неравенство 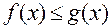 , то справедливо неравенство
, то справедливо неравенство
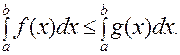
7. Если в определенном интеграле верхний предел положить равным переменной 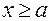 , то такой интеграл становится функцией от х:
, то такой интеграл становится функцией от х:
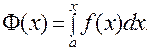 ,
,
а производная этой функции равна значению подынтегральной функции в точке х.
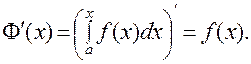
|
8. Теорема о среднем.
Если функция f (x) непрерывна на отрезке [a, b], то существует точка 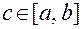 такая, что справедливо равенство такая, что справедливо равенство 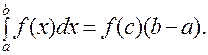
|
5.5.3. Формула Ньютона – Лейбница
Формула Ньютона – Лейбница связывает неопределенный и определенный интегралы, сводит нахождение определенного интеграла к нахождению неопределенного интеграла (точнее, первообразной подынтегральной функции) с последующей подстановкой пределов интегрирования.
Если функция f (x) непрерывна на отрезке [a, b], а функция F(x) – какая-либо ее первообразная, то
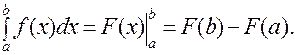
|
ПРИМЕР:
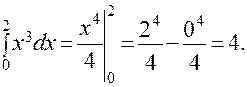
Использование формулы Ньютона-Лейбница возможно и в случае вычисления определенного интеграла методом замены переменной.
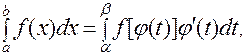
|
где новые пределы интегрирования в правом интеграле находят по формуле обратной замены 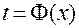 , т.е.
, т.е. 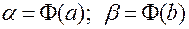 , и не требуется в результате обратного перехода к первоначальной переменной интегрирования.
, и не требуется в результате обратного перехода к первоначальной переменной интегрирования.
ПРИМЕР:
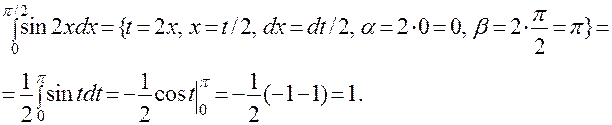
При вычислении определенного интеграла по частям также используется формула Ньютона-Лейбница.
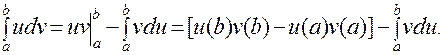
|
ПРИМЕР:
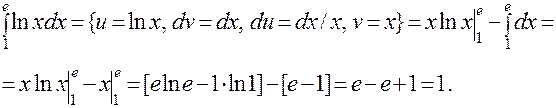
Дата добавления: 2016-04-11; просмотров: 744;
