Понятие дифференциала функции

Пусть функция y = f (x) определена на промежутке Х и в некоторой окрестности точки 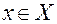имеет конечную производную:

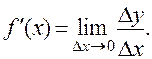
Определение. Дифференциалом функции y = f (x) называется величина .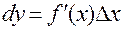

Смысл дифференциала функции заключается в том, что он приблизительно равен приращению функции Δy и пропорционален приращению аргумента Δх.

Геометрический смысл дифференциала функции следует из рассмотрения рис. 14. На нем приращение функции Δy = ΙPNΙ, а из рассмотрения треугольника MNQ следует равенство:

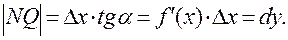
Таким образом, длины отрезков 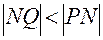, а это и означает, что геометрически дифференциал функции в точке х₀ есть часть приращения функции, отсекаемая касательной к графику функции в точке M(x₀, f (x₀)).

Рис. 14.

Для функции y = x очевидно 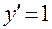, поэтому 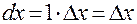, т.е. дифференциал аргумента равен приращению аргумента. С учетом этого равенства дифференциал можно записать в виде:

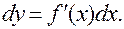
ПРИМЕР: Найти и сравнить приращение и дифференциал функции y = 2x² – 3x при х = 10 и Δх = 0,1.

Вначале найдем выражения для приращения и дифференциала функции:

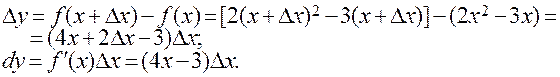
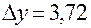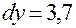Подставляя в полученные выражения заданные числовые значения, получим: и . Различие между полученными значениями не превышает 0,02 или 0,5%.

Рекомендуемая литература по теме 4:[1 ÷ 3].

ВОПРОСЫ для самопроверки знаний по теме 4:

1. Пусть производная функции в точке х = 2 равна 1. Под каким углом к оси Ох расположена касательная к графику функции при х = 2?

____________________________________________________________

2. Пусть 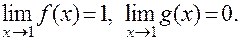Можно ли применить правило Лопиталя для нахождения предела отношения этих функций в точке х₀ = 1?

____________________________________________________________

3. Пусть производная некоторой функции на интервале (1, 5) постоянна и равна 2. Будет ли эта функция возрастающей на этом интервале?

____________________________________________________________

4. Имеет ли функция y = 1 – x² глобальный экстремум?

5. Сколько экстремумов имеет функция y = sin x на отрезке [0, 2π]?

____________________________________________________________

6. Имеет ли функция y = 5x – 7 экстремумы на отрезке [0, 3]?

____________________________________________________________

7. Пусть график функции y = f (x) на некотором промежутке имеет направление выпуклости вниз. Будет ли иметь такое же направление выпуклости график функции y = λ∙ f (x) при λ < 0?

8. Пусть прямая y = 2x + 1 является наклонной асимптотой графика некоторой функции при х→+∞. Можно ли утверждать, что такую же наклонную асимптоту график этой функции будет иметь при х→ - ∞ ?

____________________________________________________________

9. Имеет ли график функции y = 2 – x какие-либо асимптоты?

10. Пусть левый предел некоторой функции в точке х₀ = 2 равен 5, а правый предел в этой же точке – плюс бесконечности. Будет ли прямая х = 2 вертикальной асимптотой графика этой функции?

____________________________________________________________