Правила дифференцирования
1. Производная постоянной функции равна нулю, т.е.
|
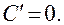
2. Производная аргумента равна единице, т.е.
|
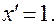
Если заданы две дифференцируемые функции u = u (x) и v = v (x), то для них справедливы следующие правила:
3. Производная алгебраической суммы функций равна алгебраической сумме производных этих функций, т.е.
|
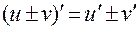
4. Производная произведения двух функций равна:
|
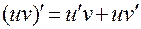
5. Постоянный множитель можно выносить за знак производной:
|
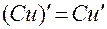
6. Производная частного двух функций (при условии v (x) ≠ 0) равна
|
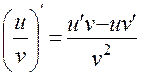
7. Если функция x = φ (t) имеет производную в точке t0, а функция y = f (x), в свою очередь, имеет производную в соответствующей точке x0 = φ (t), то сложная функция y = f [φ(t)] имеет производную в точке t0, которая вычисляется по формуле:
|
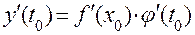
8. Если функция y = f (x) имеет в точке х0 производную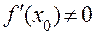 
, то обратная ей функция x = φ (y) также имеет в соответствующей точке y0 = f (x0) производную, которая вычисляется по формуле:
|
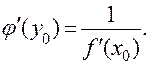
Таблица производных элементарных функций
| Функция y | Производная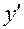 
| Функция y | Производная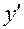
|
| 
| 
| 
|
| 
|
| 
|
| 
| 
| 
|
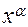
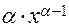
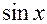
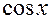
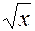
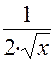
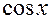
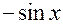
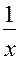
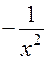
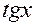
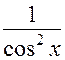
| С |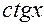 
| 
| |
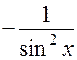
| ex | ex |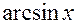 
| 
|
| 
| 
| 
|
| 
| 
| 
|
| 
| 
| 
|
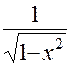
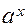
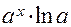
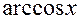
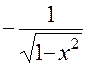
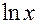
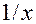
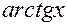
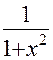
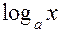
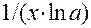
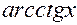
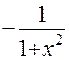
Дата добавления: 2016-04-11; просмотров: 1066;